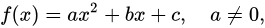O objetivo da estatística é parametrizar a realidade, contextos, populações, historiar o passado, acompanhar o presente e projetar o futuro, baseada em regras determinísticas, prováveis e precisas de causa e efeito, identificadas por parâmetros.
A estatística é uma ciência que aplica métodos científicos para garantir que o processo de análise de dados e informação seja correto e consistente.
Usa ferramentas científicas, como funções matemáticas, para representar modelos estatísticos (distribuições de probabilidades), para fazer comparações e correlações exatas entre amostras de dados.
Parâmetros são definidos, modelados ou atrelados a funções matemáticas, que explicam a subjacência ou “relações mais profundas” envolvidas no sistema.
A parametrização matemática e estatística permite garantir e controlar padrões, níveis de serviço e melhorias constantes.
Parâmetro
Parâmetro é um conceito matemático para quantificar, ajustar e comparar um modelo teórico que representa um sistema ou uma população específica na estatística.
Parâmetro é uma medida ou característica que ajuda a definir e categorizar um sistema (evento, projeto, objeto, situação, etc.).
É um componente que constrói a estrutura de um modelo ou sistema baseado em distribuição de probablidade.
Não é uma variável aleatória, mas pode ser determinado tendo como base medidas de tendência central da estatística, como média, variância ou desvio padrão.
É um componente de uma equação, ou fórmula matemática ou não matemática.
Parâmetros não representam medições ou atributos reais, mas quantidades que definem um modelo teórico, são coeficientes da equação explícitos ou implícitos.
Compõem as regras e raciocínio inferencial de um sistema.
São usados na previsão e tomada de decisão em qualquer ciência, seja matemática, física, quimica, gestão, marketing, vendas, etc.
Parâmetro é uma norma determinada e aprovada pela maioria, ou por uma autoridade, usada como base para estabelecer comparações.
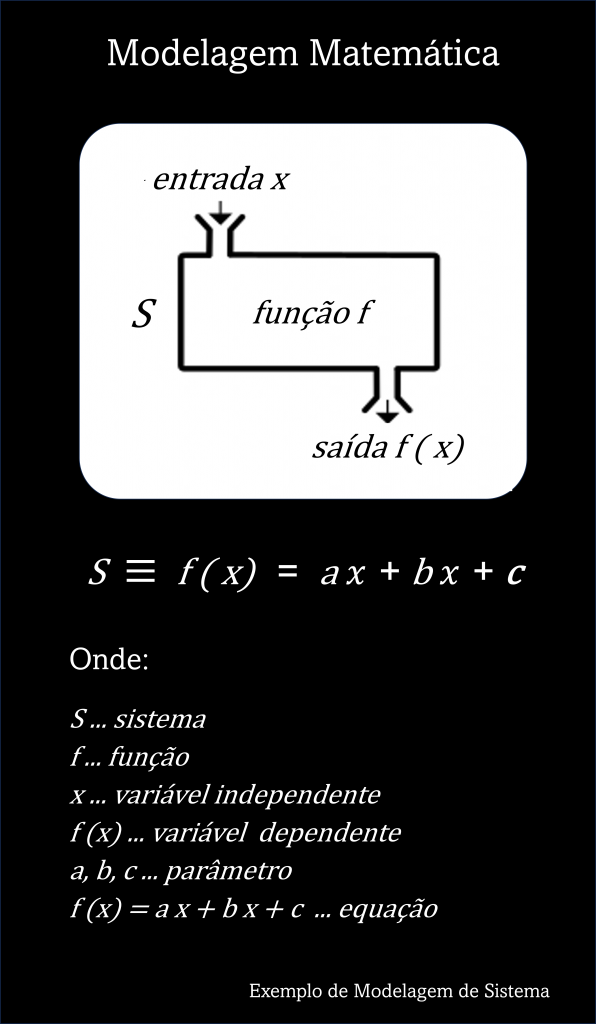
Quando um sistema é “modelado matematicamente por equações”, os “valores” que descrevem o sistema são chamados de parâmetros.
Parametrização.
Parametrização é a escolha conveniente de parâmetros ( ou medidas ) para analisar e dimensionar sistemas e gerar parâmetros.
A boa parametrização significa modelo ajustado, medições mais precisas, mais informações e indicadores sobre tendências subjacentes em seu conjunto de dados.
Descreve os elementos críticos do sistema … considerados essenciais, indicadores de desempenho, que definirão capacidades, faixas de tolerância, gargalos, previsibilidade de filas e níveis de serviço.
A parametrização é uma atividade central da modelagem de sistemas e resolução de problemas, permite modelar para simular sistemas físicos, empresariais e de negócios.
Parametrizar significa também argumentar … expor argumentos ou parâmetros para concluir ou basear um resultado ou categoria de resultado.
A parametrização torna possível fazer comparações … estabelecer comparações, identificar semelhanças, diferenças, entre coisas, pessoas, comportamentos.
Exemplos de uso de Parâmetros
Parâmetros são componentes da ciência, modelagem e métodos científicos.
Estatística … criar modelos estatísticos representar características populacionais, medi-las e usar como referência.
Identificar tipo de distribuição de probabilidade de ocorência de eventos … descrever o comportamento aleatório de um fenômeno, tal como média, mediana, moda e variância.
Modelagem específica … personalizar um modelo genérico em específico para refletir melhor a situação específica.
Estatística inferencial … obter uma afirmação acerca de uma população com base numa amostra; fazer previsões; usar a análise de dados para inferir propriedades da distribuição de probabilidade subjacente.
Comparação e variação de amostras … relacionar o desvio padrão com a média da amostra, medir a dispersãoe do quão distante cada valor desse conjunto está do valor central (média) e avaliar o nível de precisão e incerteza das previsões.
Fazer suposições … testar hipóteses válidas, testar significância de conjuntos de dados, testar uma afirrmação e tirar conclusões mais precisas sobre a população subjacente (população representada pela amostra).
Parametrização Estatística
Na estatística, as medidas de tendência central e desvio padrão são estimativas amostrais e são propriedades da coleção de indivíduos.
Para a teoria de distribuição de probabilidade, a média e o desvio padrão são chamados de parâmetros.
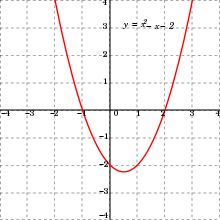
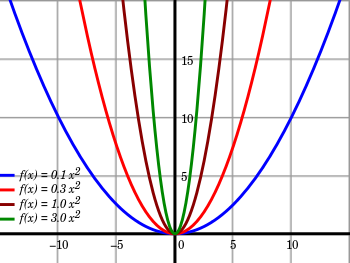
Parâmetros na estatística definem “famílias de distribuição de probabilidade”, que podem ser parametrizadas tal como ilustrado na figura, que descreve curva normal de distribuição de probabilidade e seus parâmetros.
Cada família de distribuição de probabilidade é definida por sua média e desvio padrão, ou seja, os parâmetros que especificam a distribuição normal teórica particular com a qual estamos lidando.
A maioria dos métodos estatísticos, são chamados de paramétricos porque estimam parâmetros de alguma distribuição de probabiliadde teórica subjacente.
Métodos não paramétricos, não assumem nenhuma família particular para a distribuição dos dados e, portanto, não estimam nenhum parâmetro para tal distribuição.
Exemplo do uso de parãmetros na modelagem estatística
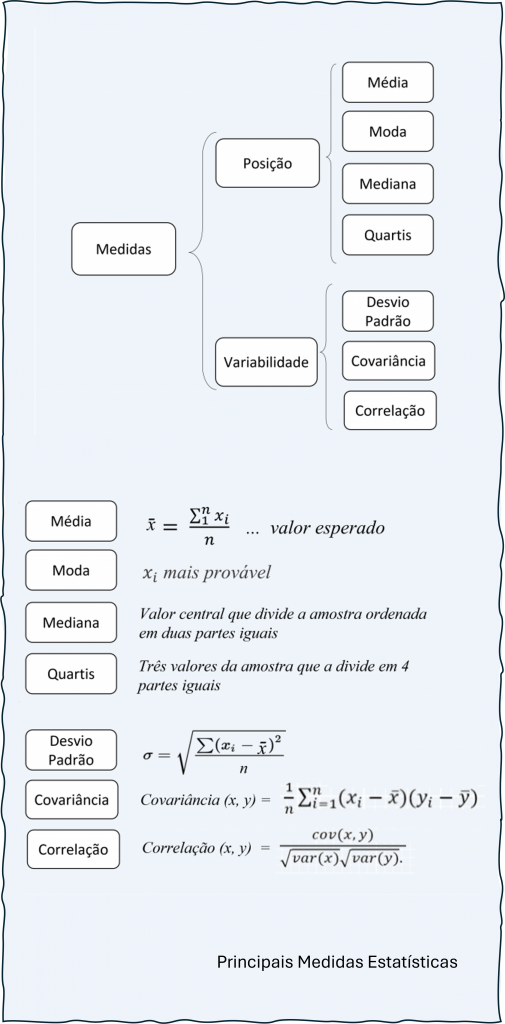
As medidas de tendência central – média, mediana, moda – são usados como parâmetros para descrever o comportamento da ocorrência de dados (ou valores) de uma amostra populacional.
O “tamanho médio de uma populaçao de indivíduos” é um parâmetro porque afirma algo sobre a população – o valor esperado mais provável de ocorrências.
A média (ou esperança estatística) nem sempre é um parâmetro adequado, porque é incompleto, demanda mais informações estatísticas sobre a amostra para podermos descrevê-la e comparar com outras amostras, fazer previsões e à partir daí, tomar decisões. Duas amostras com a mesma média podem ser completamente diferentes.
A mediana e a moda ajudam, junto com a média. melhor interpretar e comprendender o comportamento da amostra.
Já o desvio padrão adiciona mais significado e diz respeito a aleatoriedade e confiança nas previsões.
Parâmetros e Parametrização Matemática
Em modelagem e simulação de sistemas, os parâmetros são valores que podem ser alterados para ver o que acontece com o seu desempenho..
Por exemplo … o desempenho de um sistema de produção depende de vários parâmetros.
Quão o sistema mudará se “o tempo médio de serviço” reduzir ou aumentar?
Nesse cado o “tempo de serviço” é um parâmetro, que sumariza valores observados em um conjunto real de dados de produção.
Outros parâmetros podem ser: taxa de sucesso, tempo de serviço, tamanho da fila, tempo de fila, e assim por diante.
Variáveis aleatórias são quantidades que variam de indivíduo para indivíduo.
Parâmetros são variáveis que variam de sistemas para sistemas, são valores que definem e calibram um modelo teórico.
São coisas diferentes.
Parâmetros definem padrões que servem como medidas de sistemas, critérios, modelos, normas, regras, referências, indicadores, paradigmas.
O objetivo da estatística é parametrizar a realidade, contextos, populações, historiar o passado, acompanhar o presente e projetar o futuro, baseada em regras determinísticas, prováveis e precisas de causa e efeito, identificadas por parâmetros.
A parametrização permite garantir e controlar padrões, níveis de serviço e melhorias constantes.
Parametrização é a escolha conveniente de parâmetros para analisar e dimensionar sistemas.
Na estatística, as medidas de tendência central e desvio padrão são chamados de estimativas amostrais e são propriedades da coleção de indivíduos, que podem ser usados como parâmetros para descrever o comportamento da ocorrência de dados de uma amostra populacional.
Em modelagem e simulação, os parâmetros são valores que podem ser alterados para ver o que acontece com o desempenho de algum sistema.