Aleatoriedade e Processos Estocásticos na Empresa

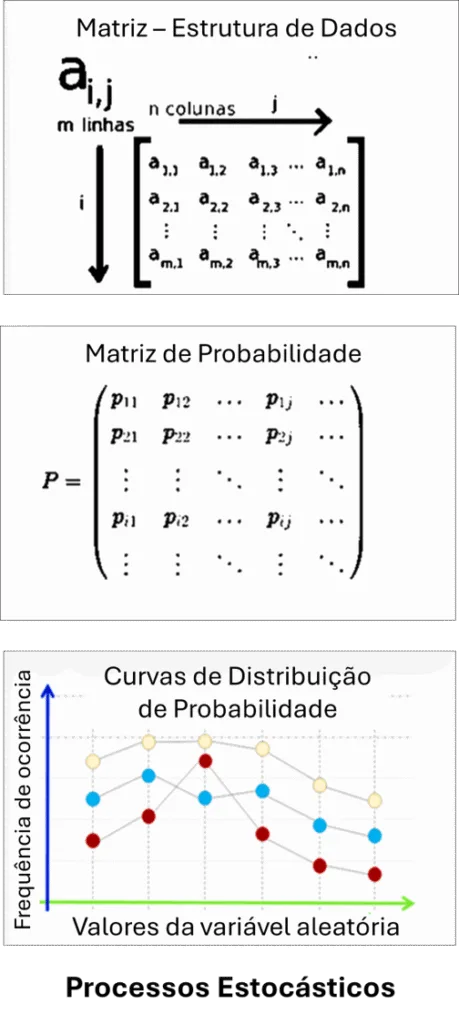
Processo estocástico … é um modelo matemático que descreve um fenômeno aleatório que evolui ao longo do tempo … é a contraparte de um processo determinístico.

• É uma coleção de variáveis aleatórias … indexadas por um parâmetro, geralmente o tempo, que pode ser discreto (como uma sequência de lançamentos de dados) ou contínuo (como a variação do preço de uma ação).
• Principal característica … o estado futuro do sistema é incerto, mas é possível calcular a probabilidade de diferentes resultados possíveis.
• Métodos Estocásticos … usam a teoria e distribuição de probabilidades para modelar sistemas aleatórios, diferindo de métodos determinísticos.
• Formalização Matemática … a estocastica combina funções aleatórias completamente diferentes no mesmo espaço amostral.
• Teoria de Conjuntos … fornece a base matemática fundamental para a teoria da probabilidade, que por sua vez é o alicerce dos processos estocásticos … os conceitos de conjuntos são usados para definir formalmente os elementos e a estrutura dos processos estocásticos.
• Teoria das Probabilidades … é o estudo matemático das probabilidades, calcula a incerteza e chance da ocorrência de eventos aleatórios.

Sistemas Estocasticos “não” são determinísticos e envolvem aleatoriedade.

• São modelos que incorporam elementos de aleatoriedade em seu comportamento, representaM sistemas que evoluem de forma imprevisível ao longo do tempo.
• São bem descritos por uma distribuição de probabilidade.
• A aleatoriedade é uma característica do mundo real e das empresas.
• Aumenta com o uso de serviços e presença humana.
• É uma medida de incerteza de um resultado.
• Deve ser considerada nas previsões de demandas e cargas de trabalhos dos sistemas, para dimensionar recursos, produtos e serviços.

---

1. Aleatoriedade … é a condição de incerteza e imprevisibilidade … métodos estocasticos são usados para minimizar impactos negativos , maximizar oportunidades, otimizar recursos, evitar sobrecargas e congestionamentos, fazer previsões, identificar riscos, prever possiveis eventos incertos, como flutuações, falhas, circunstâncias e situações, contingenciar (planos B), diversificar e espalhar e isolar o risco de diferentes ativos, fazer simulações para testar cenários e entender melhor como a aleatoriedade pode afetar o sistema e permitir otimizar a tomada de decisões.
2. Amostragem … é a técnica de monitorar e coletar de forma padronizada, valores de variáveis em tempo real, em intervalos fixos de tempo, selecionar subconjuntos de uma população maior ( as amostras) e fazer inferências sobre a população inteira … é usada quando: 1) é inviável estudar todos os elementos da população, 2) limitações de tempo, 3) custo, 4) acesso … para tal, a amostra resultante do processo de amostragem precisa ser representativa e preservar as características importantes da população.
3. Amostra Aleatória Simples … uma amostra aleatória simples é um subconjunto de uma população estatística em que cada membro do subconjunto tem a mesma probabilidade de ser escolhido e pretende ser uma representação imparcial de um grupo … ver investopedia.
4. Cadeias de Markov … é um modelo estocastico em teoria de filas que o futuro depende apenas do estado atual, e não do histórico passado, descreve uma sequência de eventos ou estados onde a probabilidade de um evento futuro ocorrer depende apenas do estado atual, e não da sequência de eventos passados que o levaram até ali, essa característica é conhecida como propriedade de Markov ou “perda de memória”.
5. Contingencia… desenvolver planos de ação para diferentes cenários que possam ocorrer, garantir o suficiente e necessário em casos de sinistros.
6. Comunicação ... usar estuturas de dados e gráficos para informar mudanças, padrões, desvios, tendências, sazonalidades, estatísticas, médias, medianas, modas, variâncias, desvio padrão, covariâncias, distribuições de probabilidade.
7. Estatística … usar ferramentas matemáticas e estatísticas ao longo do tempo, para descrever, analisar e prever o comportamento de fenômenos cujos resultados não são totalmente previsíveis, mesmo sob as mesmas condições iniciais ou correntes.
8. Estocástico … é uma família de variáveis aleatórias representando a evolução de um sistema de valores com o tempo … pode ser representado pela Função (v1, v2, v3, … vn) … onde “v” é uma variável aleatória representada por uma função.
9. Financeiro … equacionar ou criar uma representação matemática do desempenho financeiro, do futuro de um projeto, empresa ou investimento, combinar dados históricos com projeções futuras para auxiliar na tomada de decisão de longo, médio e curto prazos, calcular e prever retorno de investimentos, tradeoffs e risco.
10. Incerteza ... métodos estocasticos análisam a aleatoriedade e sistemas para tratar com ela, exige planejar cenários futuros de demanda e ofertas, planos de contingência para o “incerto”, focar em soluções no presente, mas dependentes da avaliação da resiliência, flexibilidade e adaptação às mudanças que são constantes.
11. Logística … roteamento de recursos, otimização de rotas, gestão de estoques, previsão de demanda.
12. Marketing …  processos estocásticos incorporam a aleatoriedade e a incerteza inerentes ao comportamento do consumidor e às flutuações do mercado para prever probabilidades de resultados ao invés de resultados exatos, para otimizar estratégias, e modelar a evolução de variáveis ao longo do tempo. 
13. Modelagem Matemática … processos estocásticos combinam diferentes funções ou conjuntos de variáveis aleatórias e distribuições de probabilidade que evoluem no tempo.
14. Probabilidade …. processos estocásticos descrevem distribuição de probabilidades que possibilitam tomar decisões informadas, gerenciar riscos, prever resultados e otimização de operações, num ambiente aleatório.
15. Risco … identificar, analisar, qualificar, quantificar, prever probabilidade de ocorrència e impactos nos ativos e tarefas.
16. Economia … calcular a demanda, oferta, preço, valor, lucro, custo, investimento e ROI.
17. Engenharia … análise de sinais, controle de sistemas, simulação de redes, tráfego, taxa de chegada de serviços, tempo de serviços, cargas de tráfego, filas de espera.
18. Computação … algoritmos de otimização, aprendizagem de máquina.

Conclusão.

Processos estocásticos ou aleatóriossão amplamente utilizados em empresas para modelar e gerenciar a incerteza e a aleatoriedade inerentes a muitas operações de negócios.

Têm aplicações em muitas disciplinas, como biologia , química, ecologia, neurociência, física, processamento de imagens, processamento de sinais, teoria de controle, teoria da informação, ciência da computação, telecomunicações, mercados financeiros.

Os métodos estocásticos permitem uma tomada de decisão mais robusta do que métodos puramente determinísticos, porque incorporam e quantificam a incerteza e a aleatoriedade inerentes aos sistemas do mundo real.

Métodos determinísticos, assumem que todas as variáveis de entrada e resultados são conhecidos e fixos, não conseguem capturar a complexidade e a variabilidade do mundo real.