- A Teoria de Conjunto oferece uma “abordagem sistemática” na resolução de problemas.
- É uma ferramenta inestimável para a inteligência artificial e humana.
- É uma estrutura de dados simples, formal e robusta para representar qualquer coisa, tal como dados e operações como conjuntos e funções.
- A teoria de conjuntos, provê uma metodologia estruturada que aprimora a interpretabilidade e a confiabilidade dos modelos de inteligência artificial (I.A).
- Surge como uma ferramenta poderosa nesse esforço.
- Fornece uma estrutura para análise e processamento de dados.
- Permite identificar padrões ou relações de semelhanças entre conjuntos e elementos.
- Representar o conhecimento, através da conjuntos (categorias).
- Identificar características temporais comparando pares de conjuntos e seus elementos.
- Identificar relações invisíveis entre conjuntos e obter compreensões mais profundas.
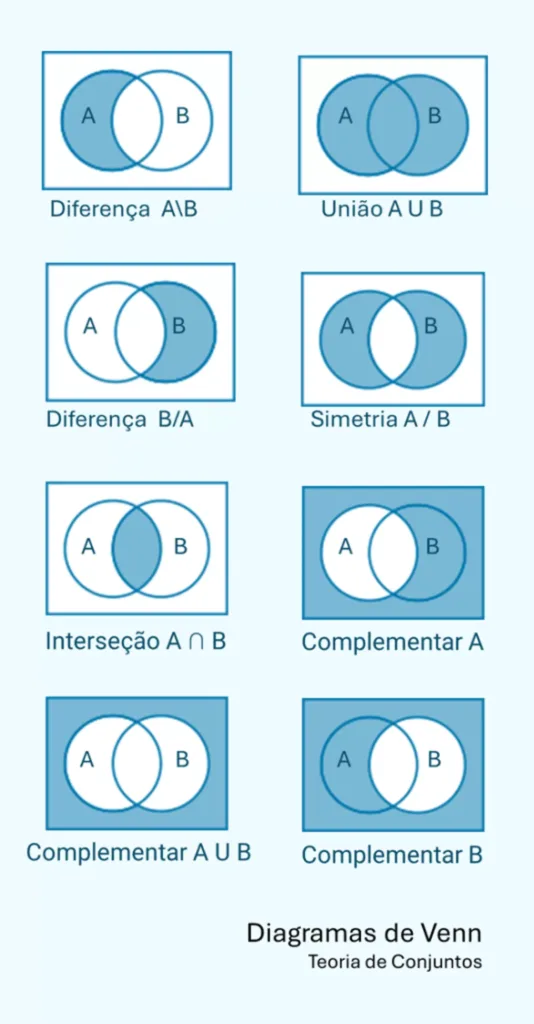
A teoria de conjuntos representa regras e relacionamentos lógicos (pertencimento, enumeração, intersecção, união, negação, complementaridade, simetria), que aprofunda a capacidade de análise, compreensão, significação de dados e informação de conjuntos de dados (amostras).
- Representar conceitos, categorias (conjuntos) e variações dessas categorias (elementos) em detalhes.
- Encontrar “agulhas num palheiro” de forma rápida e estruturada, via computação/IA.
- Identificar semelhanças e diferenças no processamento de sinais, com grandes volumes de dados por exemplo, como características específicas da voz, como pressão sonora, tonalidade, etc e reconhecer indivíduos diferentes falando a mesma frases diferentes faladaspor um mesmo indivíduo.
- Essa capacidade de representar a realidade e estruturar a resolução de problemas da teoria de conjuntos, pode ser aplicada para qualquer contexto, através de “detectores de características”.
- Para a IA, e na perspectiva de aprendizado de máquina, este é um conceito absolutamente fundamental porque funciona como ponto de partida de todos os algoritmos de aprendizado de máquina, como um método para representar eventos espaço-temporais como vetores de características.
- De uma forma geral, seguindo essa lógica, modelos de conceitos podem ser criados e estruturados dessa forma, via a teoria de conjuntos, através de conjuntos, subconjuntos, elementos e operações.
- Á partir daí, podemos dizer que conjuntos são “vetores” (e vice versa) cujas distancias para outros vetores (ou distância entre conceitos) podem ser calculadas, através da criação da “função de distância”, entre conceitos, que compara dois “vetores de características” de entrada e retorna um resultado, por exemplo, “zero” se os vetores forem idênticos e outro número se forem diferentes.
