Uma preocupação crescente com o desenvolvimento de capacidades cognitivas é estimular o raciocínio para a descoberta e a solução de problemas.
- Explorar , descobrir, associar (relacionar e conectar).
- Criar caminhos como um conjunto de conexões.
- Desenvolver e ganhar competência crítica, criatividade e a capacidade de construir e interpretar modelos matemáticos ou não matemáticos, (descritivos, normativos, deliberativos, inferenciais, preditivos).
- A aplicação de “problemas de modelação” são encarados como contextos mobilizadores de uma aprendizagem significativa.
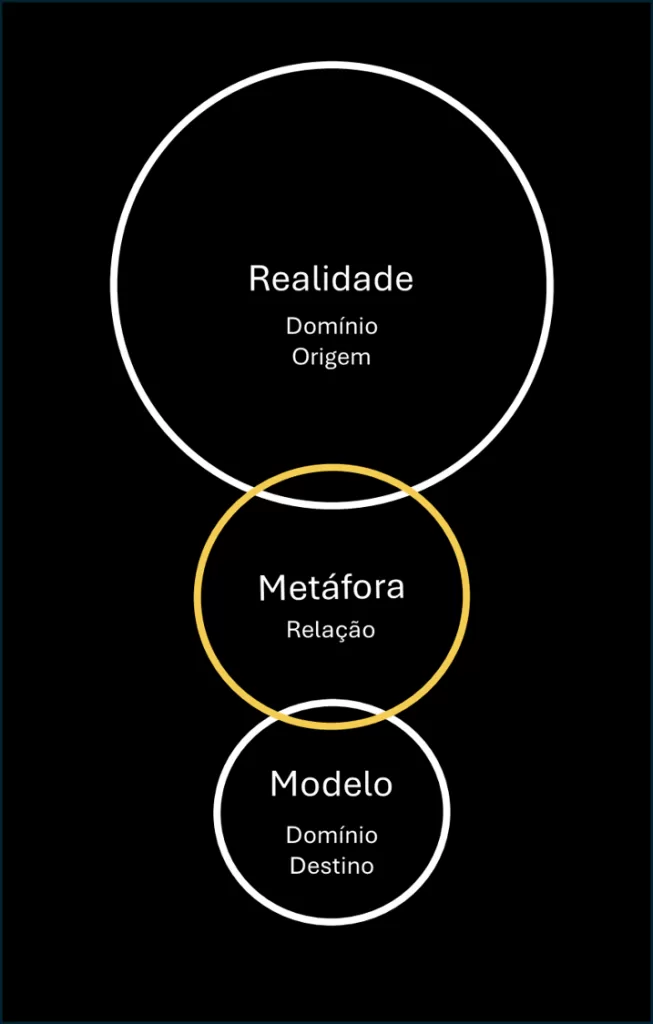
- Exige “metaforização”, ou seja, representar uma coisa por outra, conectar domínios de conhecimento e informação diferentes, ampliar significados e conhecimentos.
Principalmente na empresa, a aprendizagem deve focar em problemas de aplicação e modelos novos caminhos de trabalho e gestão de tarefas.
- Exige uma abordagem que não se esgote nos aspectos estritamente técnicos e algorítmicos da manipulação dos modelos.
- Exige reflexão coletiva (referencial) e individual (
- Qual o papel na produção e na ampliação do significado?
- Em que medida se pode falar numa base metafórica de constituição dos conceitos matemáticos?
- Que relação existe entre modelo e metáfora?
- A ligação entre conceitos e a realidade pressupõe um pensamento metafórico?
- Em que medida os problemas de aplicação de teorias, métosos e técnicas, são potenciais contextos de metaforização?
- Como é que a produção de metáforas reverte em significados e sustenta aprendizagens?
- A origem etimológica da palavra metáfora remete para translação e deslocamen-to.
- A metáfora ancora significados já constituídos da sua situação habitual e transfere-os para um novo campo referencial.
- Isto quer dizer que as significações não são formas estáveis, são relativas e dotadas de uma capacidade de variação e de um dinamismo que lhes permite servir outros referentes, impedindo que os conceitos cristalizem numa univocidade semântica (é a característica de algo que só tem um significado, ou seja, que não é ambíguo).
- (1) a metáfora tema sua razão de ser como veículo de conhecimento e contém verdades e lições.
- (2) a metáfora oculta o sentido, é escorregadia e incerta e impede a possibilidade de afirmação (a metáfora diz que alguma coisa é e, ao mesmo tempo, que não é) … radição aristotélica aconcepção de figura de estilo e de desvio da linguagem literal.
- A metáfora É um recurso essencial na construção dos nossos sistemas conceptuais.
- a verdade é que pensamose agimos com base em metáforas poderosas e penetrantes.
- A evidência sustenta aafirmação do carácter ubíquo da metáfora nas nossas formas de conceber e compreender o mundo, desde os domínios mais mundanos aos mais abstractos, levando apostular a metáfora como uma das nossas ferramentas conceptuais de aprendizageme de produção de conhecimento.
- As ideias não são guardadas em compartimentos selados.
- Ao contrário, têm a capacidade de atravessar fronteiras, de se deslocar entre domínios conceituais e de encontrar novos terrenos para germinação, assumindo novas formas criativas.
- Na metáfora, diferentes domínios conceituais – domínio-origem e domínio-alvo – são colocados em interação.
- A metáfora permite ver o domínio-alvo em termos do domínio-origem.
- Mas a qualidade projectiva das metáforas não se reduz a um fluxo de sentido único.
- A interacção constitui um dos seus atributos essenciais.
- O que isto significa é que na metáfora estamos perante um sistema de transferência de traços ou propriedades que não apenas pertencem à carga semântica de cada termo mas que abarcam os nossos conhecimentos sobre cada elemento da metáfora.
- Um dos aspectos mais importantes desta teoria é o reconhecimento de que a interacção modifica ambos os elementos conceptuais postos em confronto pela metáfora.
- A conciliação da incongruência literal com a congruência metafórica explica-se:
- Pela assimilação predicativa – o enunciado metafórico torna semelhantes, isto é,semanticamente próximos, os termos que estariam inicialmente afastados,
- Pela dimensão icónica – o pensamento metafórico é uma forma de “ver como”, isto é, uma capacidade imaginativa de mudar a nossa maneira de ver as coisas e de redescrever o mundo e
- Pela referencialidade dividida – a metáfora mantém um compromisso ambivalente com a realidade, introduzindo uma nova dimensão na percepção do reala que poderemos chamar de visão estereoscópica.
Uma última nota acerca das potencialidades cognitivas da metáfora deve fazernotar que a compreensão de um conceito pela via metafórica é algo de muito diferentede encapsular o conceito numa definição ou descrição que pretenda traduzir algumsignificado pré-determinado. A metáfora induz semelhanças e múltiplas significa-ções, faz sobressair certos aspectos do conceito ao mesmo tempo que esbate outros,mas, acima de tudo, cria conexões entre diversos conceitos. A metáfora não entregao significado correcto; ela provoca a produção de significados, na medida em queestimula um acto de compreensão (Sierpinska, 1994). O significado da metáfora nãoa antecede, antes é o resultado de uma interacção que se actualiza na colisão entrecampos semânticos díspares.Significado e aprendizagem da matemáticaFoi já referida uma das preocupações que enquadra o presente trabalho: perceberde que modo a ligação da matemática escolar ao real concorre para uma aprendiza-gem significativa de conceitos matemáticos. A questão que se coloca em seguida éa do eventual carácter pleonástico da expressão “aprendizagem significativa”. Serápossível falar-se de aprendizagem sem se falar de significado? Não será o significadoo âmago da aprendizagem, em particular, da aprendizagem de conceitos? Em quemedida a aprendizagem pode ser encarada como um processo de desenvolvimentoconceptual e, nesse sentido, como uma actividade de produção de significados? Equal é, então, o significado de significado?
- A “aprendizagem significativa”.
- Será possível falar de aprendizagem sem se falar de significado?
- Não será o significado o âmago da aprendizagem, em particular, da aprendizagem de conceitos?
- Em que medida a aprendizagem pode ser encarada como um processo de desenvolvimento conceitual e, nesse sentido, como uma atividade de produção de significados?
- E qual é, então, o significado de significado?
- A semiótica olha o mundo como se este fosse povoado de signos, mais do que de coisas.
- Palavras, textos, sinais, imagens, símbolos, gestos,formas, cores e odores, tudo o que nos rodeia, pode tornar-se, quer se queira ou não, portador de significação.
- Falar de signos é falar de um esquema conceptual complexo, feito de relaçõesentre diversos elementos.
- O processo de significação ou processo semiótico realiza-se na estrutura triádica do signo.
- Este é um dos pressupostos básicos da teoria de Charles Sanders Peirce (1978) que faz intervir o ato de interpretação no processo e significação.
- O signo é o produto da interação de três elementos: significante, referente e interpretante.
- Um signo só se torna signo quando remete para um interpretante – um signo mais desenvolvido ou uma explicação do signo inicial, isto é, um incremento cognitivo do primeiro.
- Cada interpretante pode, então, ser encarado como um novo signo e ter, portanto, o seu novo interpretante e assim por diante, num perene movimento recursivo a que se chamará de semiose ilimitada (Peirce).
Semiótica e Matemática.
- O interesse do universo sígnico e funcionamento é particularmente crucial quando abordamos o problema do saber matemático.
- A matemática é frequentemente entendida como a ciência dos símbolos, por excelência.
- Muitos defenderão até que a matemática é o paraíso em que nos libertamos definitivamente da necessidade de referência ao mundo dos sentidos.
- Mas esta posição está longe decolher unanimidade.
- Para Freudenthal (1983), por exemplo, os objectos matemáticos são criados como meios de organização de fenómenos, tanto do mundo real como da matemática.
- Os conceitos, ideias e estruturas da matemática constituem descrições organizadoras, mas o processo de criação matemática não se atém neste ponto.
- Os meios organizadores, uma vez criados, oferecem um novo campo de fenómenos que, por sua vez, poderão ser alvo de novas organizações.
- A matemática torna saliente o contínuo desdobramento de campos semânticos ou, se quisermos, uma cadeia ilimitada de relações de significação.
- Esta imagem é rica em implicações quando se deseja estudar os processos de significação de pessoas, alunos, profissionais, sobre aprendizagem de mteméticas e outras disciplinas formais (onde a forma é o foco, e não o conteúdo)
- A forma como os significados se jogam nesta semiose progressiva reforça, por um lado, o inestimável papel da interpretação e, por outro, a importância de ver nos objectos matemático meios organizadores de fenómenos, tanto do mundo real como da matemática.
- Quais são as “causas” que prejudicam ou até destroçam o significado matemático e quais as que favorecem a criação de significado nas interações em curso na sala deaula?
- A perspectiva de que a compreensão humana é metafórica na sua natureza e de que a aprendizagem é um processo evolutivo – sustentado pela possibilidade de desenvolvimento, transformação e ramificação dos significados – legitima a importância de trazer o pensamento metafórico para uma investigação da aprendizagem da matemática (e aprendizagem significativa e conceitual) enquanto processo de significação.