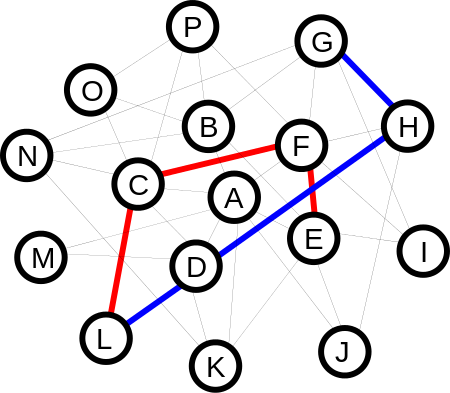
Na década de 1920, o escritor húngaro Frigyes Karinthy sugeriu que o mundo está conectado, “tal que duas pessoasem qualquer parte do mundo podem se conectar com apenas seis amizades … conhecida como teoria dos “seis graus de separação”
Essa teoria foi mito ou ficção até 1967, quando o psicólogo Stanley Milgram resolveu testar a premissa e enviou 300 pacotes para pessoas aleatórias solicitando que fizessem o pacote chegar a um homem em Boston, utilizando alguém conhecido para isso e … todas as correspondências enviadas que chegaram ao destino final passaram por seis intermediários.
Isso significa, por exemplo, que podemos chegar a qualquer pessoa na terra com mais de 7 bilhões de pessoas, numa representação de um grafo de 7 nós e 6 relacionamentos com 5 intermediários, ou seja eu e você ou qualquer pessoa pode se conectar com qualquer outra pessoa, presidente, tomador de decisão, um cliente específico, em qualquer lugar, segundo essa teoria.
Os estudos sobre a teoria de grau de separação está entre os modernos estudos de análise de redes sociais, redes neurais, arquiteturas e protocolos de rede e tabelas de roteamento de pacotes na Internet e páginas ou sites da WWW – World
Essa propriedade do mundo pequeno, passou a ser identificada nas mais variadas redes: de computadores, de interconexões entre neurônios, de estradas e aeroportos e até mesmo redes biológicas.
A teoria de redes explica as características de uma rede e permite comparar redes.
Exemplos de indicadores de rede
- Grau de complexidade da rede, função ( tempo, recurso, esforço).
- Quantidade de nós e conexões.
- Caminhos máximos e mínimos.
- Conectividade do nó.
- Conectividade da rede.
- Concentração de tráfego.
- Gargalos de tráfego.
- Distribuições de tráfego.
- Pesos de Caminhos.
É um fenômeno que parece estar em quase todas as redes e, como estas são onipresentes na natureza, podemos dizer que o mundo pequeno está em praticamente todo lugar com 6
Em 1959, antes do experimento de Milgram, os matemáticos húngaros Paul Erdős e Alfréd Rényi já haviam proposto um modelo universal de redes que incorporava essa propriedade do mundo pequeno.
Neste modelo, todos os nodos da rede –fossem pessoas, neurônios, aeroportos etc– eram igualitários, todos tinham a mesma chance de se conectar entre si.
Dado este caráter intrinsecamente probabilístico, as chamadas “redes aleatórias” mostravam que a separação entre dois nodos quaisquer é proporcional ao logaritmo do número total de nodos da rede … ou seja um modelo matemático para explicar o fenômeno, fazer previsões e parametrizar sistemas.
Então nesta época, o logaritmo era a chave por detrás do mundo pequeno, já que ele transforma números grandes em pequenos.
Por exemplo, o logaritmo de 1 milhão nos dá exatamente o mítico grau seis (na base 10)
Mesmo que o mundo tenha bilhões de pessoas, o logaritmo garante que a separação entre elas ainda assim será muito acanhada.
No entanto, qualquer modelo precisa ser adaptado à aleatoriedade específicas … por exemplo:
Uma rede social pode de fato ser descrita como aleatória?
A probabilidade de você ser amigo de um artista de cinema e de um colega da escolla é a mesma.
A possibilidade de dois de seus amigos serem amigos entre si é grande, pequena ou desprezível?
Claramente, redes sociais e outros tipos de redes não operam de modo tão aleatório.
As redes sociais aprendem e influenciam caminhos.
Albert-László Barabási e Réka Albert, propuseram em 1999 o chamado “modelo de redes livre de escala”, que desde então tem encontrado as mais variadas aplicações, desde na segurança de redes de computadores ao estudo de redes celulares e biológicas, e mesmo na otimização de estratégias de negócios, campanhas publicitárias e sistemas de aprendizagem empresarial on the job.
Uma rede sem escala é uma rede cuja a distribuição de graus (número de conexões com outros nós) segue uma lei de potência.
Lei de potência é definida matematicamente quando uma mudança relativa (quantitativa, segundo um padrão de referência) resulta em uma mudanças relativa na outra quantidade, proporcional a uma potência da mudança, independente do tamanho inicial das quantidades.
Ou seja, lei de potência é quando uma uma quantidade varia como uma potência da outra, via uma operação de exponenciação, envolvendo dois números y = x n , ode x é a base e n é o expoente ou potência, onde se lê y é igual a x elevado a n.
Exemplo … duplicar o lado “x” do quadrado (x2/x1= 2x) significa quadruplicar a área a do quadrado (2x)2 = 4x2.
Muitos fenômenos físicos, biológicos e procados pelo homem
Aplicação em várias áreas, identificação da estrutura das redes de colaboração intra e entre empresas, comunidade científica, times de trabalho, redes de cooperação e de transmissão de conhecimento,[3] páginas e sites na web,
Uma iniciativa de pesquisa recente no Brasil inclui a análise de redes de co-autoria dos pesquisadores de Ciência da Informação, denominada Rede CI.