Existem muitos cenários e situações na vida e na empresa, em que a aleatoriedade, não permite prever o valor de uma quantidade diretamente e nesses casos usamos “distribuição de probabilidades” e médias para “mostrar uma aproximação de valor“, uma tendência central de uma amostra de dados, que são coletados de observações e medidas ao longo do tempo.
Nesta introdução são listados conceitos essenciais da estatística que está na base dos métodos quantitativos, analises de dados e tomadas de decisão em muitos domínios de conhecimento na empresa.
Ou seja …
Analise e previsões econômicas – macro (ambiente) e micro (empresa).
Seleção e análise de indicadores de tempo real, para fundamentar a estratégia e operações da empresa.
Indicadores financeiros …
, demanda, preço, recursos, insumos, ativos,
Estatística … é uma ciência, mais do que um ramo da matemática.
Aplica técnicas de parametrização, padronização, estruturação e modelagem para representar a realidade, diferentes fenômenos e contextos.
Teoria Estatística …
Fornece os fundamentos de métodos de análise para tomada de decisões, baseadas em fatos e dados.
Suporta inferências, deduções e induções estatísticas.
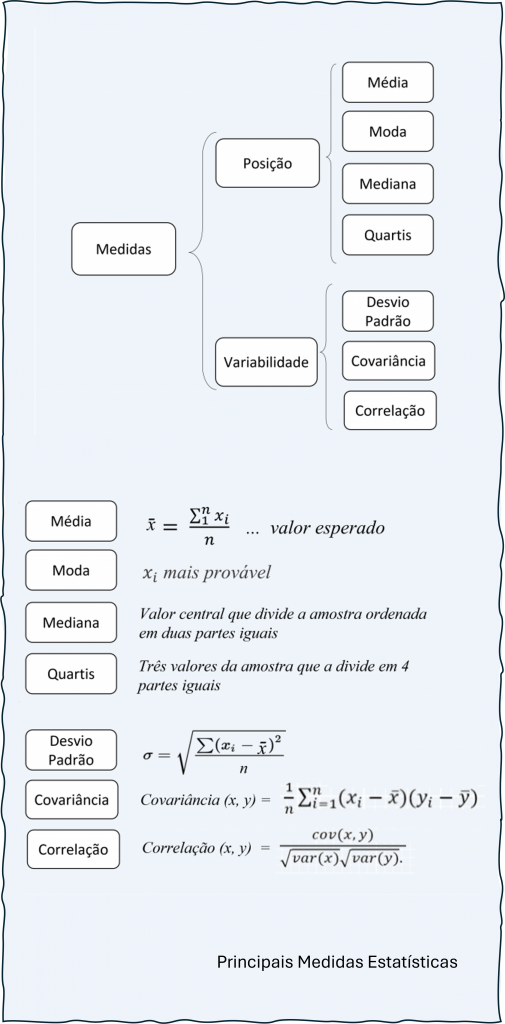
Considera tendências centrais, como média, mediana e moda.
Analisa a covariância e correlação entre váriáveis aleatórias.
Provê mecanismos matemáticos para comparar procedimentos estatísticos e alternativas.
Teoria da Probabilidade
Ramo da matemática que trata da descrição numérica da ocorrência de um evento ou se uma proposição pode ser verdadeira.
A probabilidade é um número entre 0 e 1; onde 0 é impossibilidade de ocorrência e 1 é certeza de ocorrência.
É um ramo da matemática.
É diferente das técnicas de coleta de dados estatísticos.
Parametrização
Parametrização diz respeito a aplicação da álgebra e geometria, para definir regras, princípios, relações e comparações entre variáveis, conjuntos e estatísticas, que permite criação de novos parâmetros secundárias à partir dos primários.
Padronização
A padronização é usada na “ciência da medição” (metrologia) como referência fundamental para o sistema de medidas para servir de comparação técnica.
Um padrão é baseado em consenso de empresas e governo.
Visa garantir a compatibilidade, interoperabilidade, segurança, repetibilidade, reprodutibilidade e qualidade .
O estudo e aplicação de medidas está a cargo da metrologia.
A metrologiae adoção de padrões é a base fundamental para a competitividade das empresas.
Assegura a exatidão no processo produtivo e a qualidade de produtos e serviços.
É essencial para avaliar a conformidade de produtos e processos, impulsionar a inovação e a competividade, e garantir reconhecimento no mercado.
Os principais objetivos da metrologia são traduzir a confiabilidade dos sistemas de medição, garantir condições de aceitabilidade consistentes para produtos e melhorar o nível de serviço e consumo com qualidade, preservação da segurança, saúde e meio ambiente.
É uma metodologia e que usa ferramentas imprescindíveis para o desenvolvimento e crescimento sustentável de diversos setores econômicos.
O uso de padrões visam garantir a qualidade do produto final, aumentar a confiança do cliente, diferenciar tecnologicamente e comercialmente a empresa, reduzir o consumo e desperdício de matéria-prima, aumentar a produtividade, evitar rejeição de produtos e preservar a imagem da empresa no mercado.
Amostragem
K … partição do espaço amostral
wi … conjunto de eventos com resultados possíveis em K.
X (wi) …variável aleatória que é uma função de probabilidade, que associa cada evento wi na partição do espaço amostral K, a um único número real.
Exemplo de variável aleatória X … taxa de chegada de serviço, tempo de atendimento de serviço, carga de trabalho,
Uma amostra estatística é a seleção de subconjuntos de dados K para representar uma população de indivíduos.
Fundamentalmente precisa garantia de qualidade de método de pesquisa e coleta de dados para estimar as características do “pontos amostrais” wi.
Precisa ser um conjunto de dados manejável no ambiente de tarefa da empresa.
É uma técnica de custos baixos e aplicação rápida e inteligente que evita trabalhar a população interira que seria improdutivo, caro e inviável.
De tal forma, os elementos da amostra são conhecidos como “pontos amostrais”.
A amostra é o conjunto de dados que serão feitas as estatísticas
A amostragem é uma atividade que demanda ciência e critério
Observação:
amostra … é o conjunto de dados coletados e selecionados de uma população estatística, através de um processo bem definido.
Os elementos da amostra
amostragem … metodologia da pesquisa quantitativa para gerar amostras.
Serve de base para fazer inferências, por:
- analogia … relações com semelhanças causais, parametrização semelhante; precisa de conformação por dedução, indução e abdução.
- dedução (inferir do geral para o específico), indução (inferir do específico para o geral) , abdução (dos efeitos para a causa).
A Estatística trata essencialmente de encontrar padrões e relacionamentos entre variáveis e gerar gráficos.
Quando plotamos pontos em um gráfico, fica mais fácil tirar conclusões sobre tendências e correlações entre as variáveis.
Isso é possível por meio da combinação de duas ideias-chave: probabilidade e inferência .
Probabilidade diz o que provavelmente acontecerá dada determinadas condições.
Inferêmcia permite generarlizar a pertir dessas observações ( probabilidades ) e fazer previsões.
Dois termos comumente confundidos na linguagem estatística são variável e parâmetro.
Média
A média serve para calcular o valor esperado da amostra, com uma determinada taxa de erro ou precisão com “apenas um número” … isso em estatística é chamado “tendência central”.
Exemplo do uso da média … ” em média nós ganhamos R$ 3,5 ” , ” em média o trem passa as 3,5 hs “, “em média a soma dos resultados de arremessos de um dado é igual a 3,5.
No entanto a média não capta as variações de valores do espaço amostral, nas várias medidas feitas, para se calcular a média.
Por exemplo, o espaço amostral, X = {1, 2, 3, 4, 5, 6}, po ser usado como um exemplo de possíveis resultados de medidas de um experimento ou de uma observação.
Pode representar valores de arremesso de um um dado, e pode ser também um exemplo “do que nós ganhamos” ou “o horário médio da pasagem do trem.
… esse é um aspecto importante da estatística … é matemática, aplicada de forma padronizada, estruturada e modelada para representar a realidade e diferentes fenômenos e contextos … serve de base para fazer diferentes tipos de inferências, por analogia (semelhanças causais), dedução (inferir do geral para o específico), indução (inferir do específico para o geral) , abdução (dos efeitos para as causas).
A média = soma dos valores ÷ nº de valores.
No conjunto {1,2,3,4,5, 6}, que pode representar um dado não viciado, a média é (1+2+3+4+5+6) / 6 = 3,5.
No entanto, o conjunto {1, 1, 2, 5, 6,6}, (1,1,1,6,6,6)
Interpretação da Média
Média é uma versão calculada e dinâmica de uma população X: soma os valores de uma amostra X e divide por sua quantidade n .
Tipifica uma amostra, msmo que não capte
Provê perspectivas para avaliar as variações sem comparar elementos par a par.
A média permite calcular a mediana e moda.
A mediana é o posicionamento da média
lcular a mediana e a moda, de uma amostra de dados.
É um indicador que permite junto com a variância ou desvio padrão (indicadores de distrinuição), identificar e categorizar variações, numa amostra de dados e o seu valor relativo.
Em outras palavras, a média só é efeitiva quando ascociado a varianâncias pequenas.
A efetividade da análise de dados e aplicação estatística da média, mediana e moda, só é efetiva quando associada ao desvio padrão da amostra.
Observar que a soma de todas as variações é sempre zero.
grupo
Media, Moda e Mediana são medidas de tendência central.
As três medidas represnetam uma amostra de dados com apenas uma valor.
Média
A média (Me) é uma “medida estatística central”, que é muito usada para representar amostras de dados, que é calculada somando-se todos os valores de um conjunto de dados e dividindo-se pelo número de elementos deste conjunto.
Por exemplo … a média do conjunto {1, 2, 3, 4, 5, 6} é (1+2+3+4+5+6) / 6 = 3,5
A média é mais efetiva e útil, quando a amostra de dados é uniforme com valores próximos (baixa variância).
É principalmente aplicada para situações onde:
- comparar diferentes quantidades de mesma categoria.
Desvantagem
Ocultar a variâncias(ou discrepâncias) dos valores da amostra.
Pouco efetiva para amostras de variância alta.
Bastante efetiva para amostras de variância baixa.
- identificar, quantificar, categorizar conjuntos.
- dar o mesmo “tratamento de valor”.
- quantificar valor de referência (categoria) para um conjunto, definir meta.
Média e Valor esperado
Valor esperado de uma variável aleatória
média e da sua relação com o valor esperado de uma variável aleatória (como por exemplo o retorno de uma ação no dia seguinte). Matematicamente, a média e o valor esperado são calculados da mesma forma, mas a interpretação é diferente.
Falamos em média quando nos referimos a algo que já aconteceu.
Falamos em valor esperado ao nos referirmos a uma variável aleatória que virá a acontecer.
No lançamento de um dado, por exemplo, que é um evento aleatório, temos seis resultados possíveis, {1, 2, 3, 4, 5}, cuja média é (1+2+3+4+5+6) / 6 = 3,5este valor é impossível como um resultado de lançamento.
A mesma coisa em finanças … quando falamos que o retorno mensal esperado de uma ação é 1%, queremos dizer que se obtivermos os retornos daquela ação por diversos meses, a média dos resultados tenderá a 1% … observe que não significa que esperamos que o retorno dessa ação no próximo mês seja 1%, já que é muito mais fácil de dar um valor diferente de 1%.
assim como JAMAIS esperamos que o próximo resultado do dado será 3,5. No caso do dado, 3,5 é um resultado impossível. Já no caso da ação, eu diria que 1% é um resultado bastante improvável, concorda? Isso porque há MUITO mais chances de um retorno diferente de 1% se realizar do que um retorno precisamente igual a 1%.
E é exatamente neste momento que entra o conceito de risco, intimamente ligado ao conceito de incerteza … só existe risco se houver incerteza.
O conceito de risco dependerá do seu objetivo, mas a sua quantificação é feita no mercado pelo desvio-padrão, que é uma medida de incerteza.
Agora imagine que o investimento tenha retorno de 1% ao mês e tenha distribuição normal …
Variável Aleatória.
Uma variável aleatória (quantitativa ou estocástica) é uma variável cujo resultado (valor) depende de fatores aleatórios, que significa a falta aparente ou real de padrão ou previsibilidade nos eventos … uma sequência aleatória de eventos, não tem ordem e não segue um padrão ou combinação inteligível.
Exemplos.
- Tempo médio de serviço.
- Tempo médio de produção.
- Tempo médio para reparo (MTTR).
- Tempo médio entre falhas (MTBF).
- Ticket médio de venda.
- Tempo médio de chegada de serviço.
- Tempo médio de espera na fila.
- Preço médio de produtos.
- Nível médio de qualidade de serviço.
- Carga de Trabalho média
Moda
Moda Mo representa o valor mais frequente da amostra de dados, ou mais provável de ser amostrado.
Assim como a média e a mediana, a moda é uma forma de expressar, em um número único, informações importantes sobre uma variável aleatória ou uma população .
Mediana
Mediana Md representa um valor central da amostra, em termos de posição e localização, após ordená-la de forma crescente ou decrescente.
- É o valor que separa a metade maior e a metade menor da amostra (ou conjunto, população,distribuição de probabilidade).
- Ex. Para o conjunto {1, 2 ,3, 4, 5} a mediana é o valor do meio, no caso 3 … para o onjunto com número par de elementos, {1,2,3,4,5,6} a mediana é a media (3 + 4) / 2, que é igual a 3,5.
Aplicações da Mediana
- Identificar distorções ou possíveis falhas de medição ou coleta de dados da amostra.
- Identificar o valor que divide a distribuição de probabilidade em duas metades iguais.
- Ignorar eventos estremos de uma amostra
- Encontrar a maioria dos dados intermediários.
Tal como a média, tem vários tipos.
Retornar a tendência central em tendências numéricas distorcidas.
Desvio Padrão
Desvio Padrão é a raiz quadrada da variância ou dispersão de uma amostra de dados em relação à sua média (valor esperado).
É uma medida estatística frequentemente usada para testar modelos e comparar dados do mundo real, variações, precisões, consistência, incerteza, risco e retorno do investimento.
Na produção … é usado em varias situações: para determinar se o peso, preço, tamanho médio de um produto, está dentro de uma faixa de tolerância.; produção precisará ser interrompida ou retardada, ou o produto precisar ser aberto, pesado ou ser usado no teste.
Em finanças … medir o risco de um determinado ativo, atrelado a flutuações de valores, preços e retorno de investimentos; avaliar a incerteza dos retornos futuros; se maior variância, incerteza e risco e avaliação de maior retorno do investimento.
Uma propriedade útil do desvio padrão é que, ao contrário da variância, ele é expresso na mesma unidade que os dados.
Depende de eventos probabilísticos, de posíveis resultados em um espaço amostral.
Um grande desvio padrão indica que os pontos de dados podem estão afastados da média e um pequeno desvio padrão indica que eles estão agrupados próximos à média.
É uma medida de incerteza.
O desvio padrão de um grupo de medições repetidas fornece a precisão dessas medições e concordância com as previsões teóricas.
Se a média das medições estiver muito longe da previsão (com a distância medida em desvios padrão), os testes precisam ser revisado, estão fora da faixa de tolerância.
Covariância
