Modelagem Matemática na Empresa

A “matemática não acadêmica” ou “matemática empresarial” deve ser encorajada na empresa.

• Propósito … é um conhecimento fundamental ​​para resolver problemas, avaliar oportunidades e valores, relacionados aos negócios. 
• Natureza ... a matemática é uma ciência inerentemente quantitativa, mas pode ser usada como ferramenta qualitativa.
• Tipos de Dados … trabalha com dados qualitativos e quantitativos.
• Dados qualitativos … descrevem um assunto, um modelo ou esquema, não são expressos em números, mas podem ser analisados e medidos qualitativamente, através de proposições e relações, são organizados em categorias nominais (via nomes) ou ordinais (via ordem).
• Dados quantitativos … definem um assunto e são expressos como um número, pode ser quantificados e analisados.
• Existem dois tipos de dados quantitativos na matemática contínuos e discretos.

Matemática … Abordagem Qualitativa.

O lado qualitativo da matemática está na “modelagem e técnicas de solução de problemas” na educação, cognição, computação, gestão, estatística, engenharia, física.

A “matemática qualitativa” é uma abordagem ou um conceito utilizado principalmente em estatística e pesquisa para lidar com dados que representam qualidades, características ou atributos em vez de quantidades numéricas mensuráveis.

A categorização é o processo central dessa abordagem.

Ela se concentra em características como forma, ordem e simetria, e pode ser vista como sinônimo de matemática pura , que explora padrões em objetos mentais abstratos sem necessariamente exigir medição numérica.

Ao contrário da matemática quantitativa, que se baseia em medições e cálculos, a matemática qualitativa pode ser usada quando a medição direta não é adequada ou possível.

A análise qualitativa é usada para descrever a natureza e a qualidade da informação, enfatizando dados descritivos e não numéricos.

Em áreas como psicologia, economia, marketing, uma abordagem qualitativa pode descrever o comportamento geral de um sistema (por exemplo, se ele é estável ou oscilatório) sem exigir entradas numéricas exatas para cada variável.

A matemática tem várias definições …

Ciência dos padrões.

A matemática envolve ideias, conceitos, que existem apenas na consciência compartilhada dos seres humanos… é uma disciplina que estuda “objetos mentais com propriedades reproduzíveis”

As pessoas geralmente não se dão conta de que parte da matemática … O seu lado qualitativo .. é um esforço para encontrar e moldar os conceitos/definições ‘corretos’ e para formular/desenvolver as questões e os problemas ‘corretos’.

“A matemática deve lidar com situações bem definidas.

Assim, em suas relações com a ciência, a matemática depende de um esforço intelectual externo à matemática para a especificação crucial da aproximação que a matemática deve tomar literalmente (exatamente e completamente)

Formalizar um problema em terminologia precisa pode ser difícil, e alguns matemáticos acreditam que a parte mais importante da resolução de problemas envolve processos inconscientes, como a intuição.

A matemática e psicologia tem relações importantes … ambos estudam objetos que existem na mente hiumana.

Considerando que na teoria de conjuntos definiu um conjunto como “qualquer coleção M de objetos definidos e bem distintos m de nossa percepção ou de nosso pensamento”, os fenômenos psicológicos também podem ser considerados como um conjunto (se forem “bem distintos”).

Uma consequência lógica seria buscar semelhanças entre objetos matemáticos e psicológicos, de modo que objetos matemáticos possam ser usados ​​como representações de objetos psicológicos, como sentimentos, desejos, cognições, raciocínios, decisões e outros fenômenos psicológicos.

Se interpretarmos “matemática qualitativa” como “matemática pura”, o seu equivalente seria a matemática aplicada.

Ambas as disciplinas lidam com objetos matemáticos como matéria de estudo, mas seus objetivos e abordagens diferem. 

Matemática aplicada poderia ser descrita como “a ponte que conecta a matemática pura com a ciência e a tecnologia”,

William Prager.

A“a matemática aplicada não é um campo científico definível, mas uma atitude humana… onde o cientista] deve estar disposto a fazer concessões em relação à completude matemática rigorosa”.

O matemático aplicado deve se basear em… soluções especiais, descrições assintóticas, equações simplificadas, experimentação tanto em laboratório quanto no computador”. A principal diferença nos objetivos reside no fato de que, enquanto a matemática pura se concentra na compreensão teórica, a matemática aplicada se preocupa com as aplicações práticas no mundo externo.

A diferença de abordagem está em que a matemática pura busca compreender por que algo é válido, enquanto a matemática aplicada se satisfaz se fornecer resultados reproduzíveis.

A matemática aplicada não se preocupa em compreender as razões subjacentes, sendo, portanto, menos reflexiva dos aspectos teóricos.

 A “matemática qualitativa” abrange todos os objetos matemáticos. 
de Lee (2013) . Um capítulo discute sistemas dinâmicos complexos, que são sistemas que utilizam funções não lineares sobre uma estrutura quantitativa. Esses sistemas exigem a mensuração de variáveis ​​quantitativas. No texto de Lee, o aspecto quantitativo é apenas uma instância do qualitativo. O que caracteriza a matemática como qualitativa é a perspectiva que ela adota. O fator crucial é se a estrutura matemática se alinha com um fenômeno psicológico. Um termo útil para descrever o oposto dessa atitude é “ 
matemática oportunista ”. 
Stöltzner (2004) afirma que, quando uma disciplina científica possui apenas uma teoria fraca sobre si mesma e uma terminologia mal definida, os matemáticos aplicados adotam uma estratégia de portunismo matemático em relação a essa disciplina. Isso significa que eles criam situações nas quais podem aplicar suas estruturas matemáticas preferidas para representar algum fenômeno da disciplina, desconsiderando a estrutura interna do fenômeno para facilitar essa manipulação.

Matemática qualitativa como alternativa à mensuração

A mensuração quantitativa atrai pesquisadores devido à sua exatidão, precisão, rigor e clareza ( Michell, 1999 :34; Gould, 1996 ).

Ela também possibilita a padronização de processos e a tomada de decisões objetivas para empresas e governos.

No entanto, também tem enfrentado fortes críticas de muitos pesquisadores da psicologia.

Alguns psicólogos acreditam que os modelos quantitativos podem não descrever bem os fenômenos psicológicos e argumentam que a mensuração numérica adequada para a física não é adequada para a psicologia e questionam a aplicação das mesmas regras utilizadas nas ciências físicas à psicologia .

Alguns pesquisadores defendem que, em relação à matematização, a psicologia deveria ampliar seu escopo para além das abordagens puramente quantitativas e sugere que os atributos quantitativos não devem ser o foco exclusivo da investigação científica, defendendo a exploração de estruturas não quantitativas quando faltam evidências de quantificação.

Se nenhuma estrutura quantitativa for encontrada, isso deve ser visto como “o início da busca pelo tipo de estrutura não quantitativa na qual a natureza, neste caso, está organizada”..

Diante disso, grafos, gramáticas de linguagem ou autômatos podem ser empregados como estruturas não quantitativas na análise estrutural de dados.

Alguns críticos da mensuração considerar a matemática qualitativa como uma alternativa potencial, oferecendo o mesmo nível de exatidão, rigor e clareza.

O uso da matemática qualitativa exige estruturas matemáticas inerentes ao objeto psicológico,

Vamos resumir esta seção: a matemática qualitativa, ou pura, é uma disciplina que busca padrões em objetos mentais reproduzíveis, por vezes empregando terminologia imprecisa com a esperança de refiná-la no futuro.

Ela difere de sua contraparte, a matemática aplicada, por não fazer concessões quanto às relações mútuas dos objetos mentais que estuda, os quais devem ser consistentes entre si.

1. Análise de dados …
2. Categorização ... classificar os dados qualitativos em categorias nominais (rótulos, sem ordem ou hierarquia) ou ordinais ( ordem definida).
3. Estatística … coleta, organização, análise e interpretação de dados para a tomada de decisões. e brange tanto dados numéricos (quantitativos) quanto não numéricos (qualitativos).
4. Análise não Numérica … lidar com variáveis nominais (sem ordem) e ordinais (com ordem definida), qualidades e atributos, não medidos numericamente, categorização de dados não numéricos, variáveis nominais, onde hão há ordem ou hierarquia entre categorias, estatística,
5. Criatividade … processo deliberado de mudança, manipular símbolos, conceitos ou objetos para produzir um evento novo ou incomum para o sujeito ou ambiente, ganhar autonomia para produzir uma nova forma de fazer algo único e original.
6. Métodos qualitativos …
7. Comunicação … criar expressões, criar fórmulas, transcrever, analisar, desenhar ideias e raciocínios, de forma sintética, estruturada ne geométrica.
8. Formalização … usar suposições, axiomas, regras de inferência, equações, para construir e validar o conhecimento, prover precisão, consistência, universalidade e provas formais.
9. Formulação …
10. Formalização … criar normas, regras, modelos, procedimentos padronizados
11. Técnicas Aprendidas … descrever métodos, estratégias e ferramentas que um indivíduo adquiriu e domina para facilitar a aprendizagem, a memorização e a aplicação de conhecimentos ou habilidades.
12. Heurística – procedimento mental simples que ajuda a encontrar respostas adequadas, embora várias vezes imperfeitas, para perguntas difíceis … tendo como base ou pano de fundo uma matriz.
13. Exercícios … praticar e aplicar conceitos e equações matemáticas, para fixar ou desenvolver algum aprendizado, resolver um problema específico, que não requer invenção ou criação, apenas aplicação de conhecimentos.
14. Interpretação … lógica qualitativa, proposições lógicas
15. Intuição matemática … desenvolver a percepção instintiva de conceitos, que surge do repertório construído através do estudo e da prática repetida, fazer “saltos criativos”, complementada por lógica e demonstração. Para desenvolver essa intuição, é crucial resolver muitos problemas, aprender com os erros e buscar a compreensão além das fórmulas.
16. Lógica matemática …estudar a estrutura formal do raciocínio, para ser aplicada para provar teoremas e resolver problemas, analisar proposições (afirmações que são verdadeiras ou falsas) e conectivos lógicos (como “e”, “ou”, “não”) para construir argumentos matemáticos válidos.
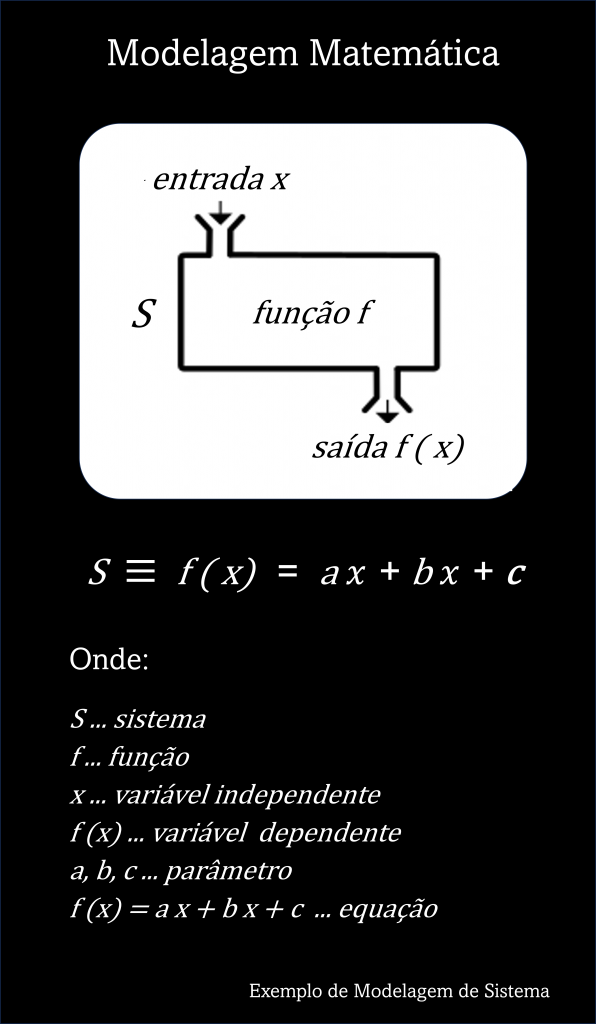
17. Modelagem qualitativa matemática … usar a matemática para entender e prever fenômenos do mundo real, começando com a observação da realidade (qualitativa) e avançando para a criação de um modelo matemático., traduzi problemas da realidade em linguagem matemática, resolver e interpreta as soluções de volta no contexto do mundo real. A parte qualitativa foca nas observações, descrições e no contexto do problema, enquanto a parte matemática envolve a criação de equações, funções e outros modelos para descrever o fenômeno.
19. Previsões Qualitativas … o lado qualitativo da matemática ajuda a escolher caminhos, fazer previsões e julgamento subjetivos, usar a lógica, intuição matemática, opinião de especialistas, dados não numéricos para estimar resultados futuros, útil quando há poucos dados históricos disponíveis … complementa a previsão quantitativa, é menos precisa, mais propensa a vieses do que a análise de fatos e dados quantitativos e históricos.
20. Problematização … analisar e modelar formas de pensar, criar, inovar, formular problemas e métodos matemáticos, avaliar se existe uma, diversas ou nenhuma solução num dado contexto e formular estratégias.
21. Formulação … criar expressões que usam números, letras e símbolos para representar relações e resolver problemas, sintetizar um raciocínio, facilitar cálculos e aplicar conceitos em diversas áreas, como geometria, álgebra, finanças e estatística.
22. Traduzir … transpor de uma línguagem para outra, representar pensamentos, movimentos, espaços por equações ou fórmulas, que possam ser visibilizadas e compartilhadas.
23. Equacionar … dispor numa equação uma ou mais incógnitas (valores desconhecidodos), representar componentes, pesos e relações para resolver um problema específicos … estabelecer um método de formular e resolver problemas, criar e avaiar hipóteses e estratégias lógicas para solucionar desafios. 
24. Organização … usar a estrutura matricial para adquiririr, armazernar, processar e apresentar dados.
25. Representar o mundo físico no mundo abstrato e vice versa de forma específica e parametrizada.
26. Focar a atenção e buscar a compreensão, e explorar o “porquê” dos resultados finais, chegar as causas.
27. Analisar dados não numéricos via conversas, observações e textos, para obter vários tipos de perspectivas e interpretações do contexto.
28. Pesquisar, compreender e comunicar uma equação descritiva da natureza de um problema, fenômeno ou solução.
29. Impulsionar o raciocínio dialético.
30. Organizar o processo de abstração e desenvolvimento de conceitos, onde o concreto leva ao abstrato em um movimento dialético.
31. Relação entre o concreto (manipulável) e o abstrato (conceitos).
32. Pensamento de Platão …  a matemática uma ciência intermediária que prepara o filósofo para a dialética, que busca o conhecimento do “Bem”.
33. Hegel: Via o progresso matemático como um processo dialético, onde novos conceitos surgem do movimento entre o concreto e o abstrato.
34. Descartes: Usava a matemática como um campo de teste para seu método filosófico, aplicando ideias filosóficas à geometria e ao raciocínio matemático. 

Forma Quantitativa de Pensar na Matemática.

A empresa deve beneficiar e tornar explícitas as ligações entre a ciência e a matemática, porque a ciência fornece exemplos concretos de ideias matemáticas abstratas e a matemática ajuda as pessoas a alcançar uma compreensão profunda dos conceitos científicos

(McBride e Silverman 1991).

Como integrar ciências e matemática na empresa?

Quase todas as investigações científicas provavelmente exigirão uma ou mais habilidades matemáticas de classificação, contagem, medição, cálculo, estimativa e registro em tabelas ou gráficos.

As estatísticas são amplamente utilizadas na ciência.

A matemática ajuda-nos a compreender a ciência e a conceber, conduzir e analisar os resultados de experiências científicas .

A ciência exige que coletemos dados, interpretemos-os em busca de padrões significativos e tiremos conclusões que aprofundem nosso conhecimento.

A matemática modela fenômenos e relações em nosso ambiente observável, ao mesmo tempo em que articula conceitos do intuitivo ao obscuro.

Em Modelagem

A maioria das empresas bem-sucedidas verifica todos os dados relacionados aos negócios, desde clientes até produtos, para decidir quaisquer mudanças ou planejar oportunidades futuras. Os conceitos matemáticos são utilizados para aprender modelos para análise de mercado e encontrar oportunidades no mercado dependendo das demandas do cliente e do número de vendas.

Em Estatísticas

Math’s é usado para criar tabelas e gráficos para resumir e verificar dados históricos em um formato organizado. Esses quadros e gráficos podem ser utilizados na reunião para discutir o crescimento ou possíveis mudanças no modelo de negócios.

Em Marketing

A matemática também é usada para criar uma estratégia de marketing de sucesso para melhorar as vendas futuras. A maioria das empresas utiliza diferentes modelos de preços para atrair clientes com orçamentos diferentes. A análise matemática é usada para criar um preço que equilibra os lucros com a demanda do cliente.

Melhorar a investigação, ensino científico e autodidatismo …

Perceber e oportunidades de de negócios … aumentar a gama de problemas percebidos do mundo real e aumentar o impacto positivo na sociedade.

Projetar mudanças … com o rápido avanço no campo da ciência e da tecnologia, as empresas modernas de produtos e serviços precisam mudar rapidamente e continuamente.

Implementar métodos mais sofisticados … a “matemática empresarial” fator está na base de modelagem de produtos e serviços e garantia de padrões de qualidade e níveis de serviço, bancos de dados, redes de computação mais econômicas, etc.

Ajuda a pensar … descobrir, entender, compreender, qualificar e quantificar o ambiente de tarefa e fundamentar modelos, para provocar e monitorar mudanças e inovações.

Em Gestão de Risco

Muitas ferramentas matemáticas são usadas para verificar riscos financeiros e mudanças futuras em um negócio. Alguns softwares também recebem informações e determinam o possível risco no negócio. As ferramentas também ajudam a estimular cenários futuros, o que ajuda a prevenir quaisquer riscos na implementação real de qualquer mudança no modelo de negócio.

A matemática na empresa enfatiza as habilidades escritas e orais, juntamente com as habilidades de trabalho em equipe, que são altamente valorizadas nas indústrias … isso porque usa uma linguagem significativa, sintética, memorável e não ambígua.

A reflexaõ e uso de conceitos matemáticos estrutura a resolução de problemas gerais e empresariais do cotidiano.

A matemática na empresa deve ser vista como um conjunto de ferramemntas que ajudam a formular, investigar, parametrizar e resolver problemas de qualquer spécie ou domínio do conhecimento.

O desenvolvimento de “competências matemáticas” são necessárias para a colaboração de trabalhadores de diferentes áreas para produzir produtos inovadores.

O ” pensamento matemático” é fonte de alta agregação de valor na empresa e sociedade, ajuda a tomar decisões, minimizar custos, escolhercaminhos, e assim por diante.