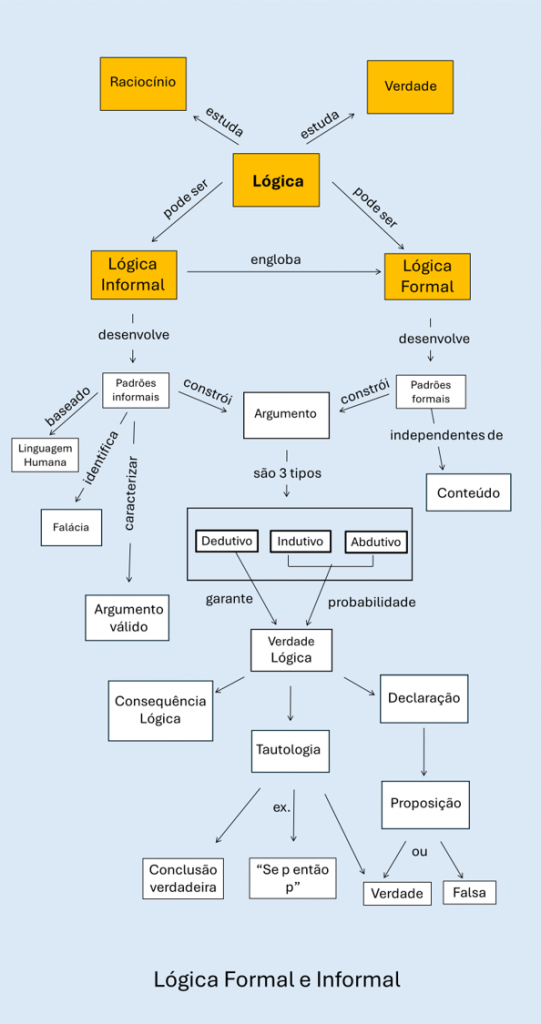
Lógica é um tipo especial de raciocínio que usa argumentos para Analogia, Dedução, Indução e Abdução.
Argumento … é um conjunto de proposições concatenadas, em sequência.
Proposição … é uma oração declarativa, que pode ser classificada como verdadeira ou falsa” , que estão relacionadas num dado conjunto de argumentos.
Exemplos de Proposições e Operações lógicas …
Seja:
p … uma proposição.
q … outra proposição.
Operações Lógicas
~p … (não p) … negação de p.
p ∧ q … (p e q) … conjunção de p e q.
p ∨ q … (“p ou q” ) … disjunção de p e q.
p⊕q … (“p ou exclusivo q”) …. dicotomia de p e q.
p→q … (se p then q) … conditional.
p↔q … (p se e somente se q) …biconditional.
A lógica e seus argumentos, operações, proposições, premissas, regras de inferências e conclusões podem ser representados de forma pictórica (gráfica, visual) pela teoria de conjuntos, com suas ferramentas e operações …
Lógica de Argumentação
A Lógica da Argumentação … é uma descrição formalizada das maneiras que o ser humano humano raciocina e discute sobre proposições.
Tem alta relação com o desempenho competitivo, emocional e cognitivo de indivíduos e empresa.
É aplicada de forma universal para qualquer tipo de conjunto, físico ou abstrato.
A lógica como ferramenta da filosofia tem relações fundamentais com a epistemologia, ética e as ciências e artes.
10 Benefícios Potenciais da Lógica
As operações lógicas estão na base da argumentação formal e da língua natural … são ferramentas para …
- Melhorar o Raciocínio … a lógica pemite analisar, sintetizar, compreender, comunicar e explicar melhor o processo de formação e uso da razão; orientar a criação de proposições, sentenças, que podem ser verdadeiras ou falsas, que podem ser concatenadas via argumentos, que justifiquem ou avaliem a veracidade de propostas e opiniões.
- Desenvolver a Razão … a lógica aumenta a capacidade de raciocinar e desenvolver a razão (capacidade de raciocinar), tirar conclusões e compreender, tal como na matemática, onde a razão é o quociente entre dois números, conceitos ou proposições.
- Focar na Forma Lógica … a lógica representa argumentos através da gramática formal e do simbolismo de um sistema lógico e explicita semelhanças ou diferenças de argumento com outros do mesmo tipo.
- Formalizar a Gramática … a lógica é usada para criar conjuntos de regras (sintaxe) que definem como formar cadeias de símbolos em uma linguagem formal.
- Formalizar a Linguagem … a lógica é fundamental para criar linguagens artificiais, desenvolvidas pelo homem e compreendidas por homens e máquinas, baseadas em regras sintáticas e endereçadas para aplicações, contextos e objetivos específicos.
- Modelar a Linguagem Natural … a lógica pode representar ou modelar características estruturais importantes da linguagem natural, usada no senso comum, na comunicação do cotidiano, como a generatividade e a composicionalidade da linguagem, explicitar critérios gerais para distinguir o bom raciocínio do mau, tal como o realizamos ou, o equivalente, tal como ele é ou pode ser expresso em argumentos declarados em alguma linguagem natural ou outra ..analisar e avaliar a linguagem natural, a forma de comunicação mais comum entre seres humanos, que é expontânea e não premeditada; seu processamento é de interesse da IA.
- Construir Sistemas Lógicos … a lógica é frequentemente estudada para construir sistemas lógicos, que basicamente listam todas as verdades lógicas, de um subgrupo da lógica, por meio de aplicações de regras recursivas, que podem ser repetidamente aplicadas e concatenadas; isto é feito identificando axiomas (verdades absolutas) e regras de inferências, dos quais podem ser inferidos teoremas e verdades lógicas.
- Criar Regras e Argumentos … entender axiomas e princípios para deduzir, induzir, abduzir, avaliar e criar proposições verdadeiras.
- Identificar Analogias … comparar conceitos e relações semelhantes para validação pela logica.
- Aumentar o Desempenho Cognitivo … a capacidade de argumentar, inferir, concluir, comunicar, provar, objetivar, afastar subjetividade
Dedução
A dedução é uma “forma de raciocínio” que produz conclusões que são logicamente implicadas por premissas mais gerais para uma mais particular.
O raciocínio dedutivo é o único que garante suas conclusões em todos os casos.
A dedução se distingue de outras formas de raciocínio, como a abdução , a indução e o raciocínio analógico.
Aristóteles reconheceu de que o que torna uma etapa da conclusão imediatamente óbvia é sua forma, e não seu conteúdo!
Não importa o assunto e sim a estrutura dos fatos com os quais você está trabalhando.
Por exemplo … 2 bananas + 2 maças = 2x + 2y … o conteúdo muda mais o formato (relações) é o mesmo.
Padrões lógicos são chamados de regras de inferência.
Outro exemplo: “todos os x são y e todos os y são z”, portanto todos os x são z.
Observe que independentemente do que x, y, z, sejam a conclusão será sempre verdadeira.
O que distingue um padrão correto de um incorreto é que ele deve sempre levar a conclusões corretas, se as premissas ( proposição que suporta outras) nas quais se baseiam, sejam corretas.
O conteúdo é importante, mas secundariamente e pode não importar ser verdade ou falso, nas tautologias lógicas.
( … tautologias lógica é um conjunto de proposições conectadas que o resultado e sempre verdadeiro para todas as possíveis valorações de suas variáveis proposicionais.
Por exemplo, a fórmula proposicional 
Existem exemplos mais complexos …
Indução
Indução é o raciocínio do particular para o geral.
Se vemos casos suficientes em que algo é verdadeiro e nunca vemos um caso em que é falso, tendemos a concluir que é sempre verdadeiro.
Exemplo:
Eu vi 1000 corvos negros.
Nunca vi um corvo que não fosse negro
Portanto, todo corvo é negro.
A indução não garante uma resposta 100% verdadeira, tal como a dedução.
Trabalha com probabilidade, que podem ser com maior ou menor.
É o raciocínio que generaliza
Abdução
Abdução é o raciocínio dos efeitos para as possíveis causas.
Muitas coisas podem causar um resultado observado.
Frequentemente tendemos a inferir uma causa mesmo quando nossa enumeração de causas possíveis é incompleta.
Exemplo:
Se não houver energia, a lâmpada não acende.
Existe energia e a lâmpada não acende.
Portanto, a lâmpada está com defeito.
A abdução é um tipo de indução.
Busca a melhor resposta, a mais simples e provável.
Analogia
O raciocínio por analogia é o raciocínio no qual inferimos uma conclusão com base na semelhança de relações entre duas situações.
Exemplo:
A vazão em um cano é proporcional ao seu diâmetro.
Fios são como canos.
Portanto, a corrente em um fio é proporcional ao diâmetro.
De todos os tipos de raciocínio, a dedução é a única que garante suas conclusões em todos os casos, ela produz apenas aquelas conclusões que são logicamente implicadas pelas premissas de alguém.





