A distribuição normal é frequentemente chamada de curva do sino porque o gráfico de sua densidade de probabilidade parece um sino.
É uma distribuição de probabilidade de grande importância nas estatísticas, porque muitos fenômenos e amostras de dados contínuos na natureza e na psicologia exibem essa curva em forma de sino, quando compilados e grafados.
Também é conhecida como distribuição gaussiana, em homenagem ao matemático alemão Carl Gauss, que a descreveu pela primeira vez.
É uma distribuição de probabilidade que é simétrica no entorno da média e os dados próximos à média são mais frequentes e prováveis.
Parâmetros importantes da curva normal
A curva normal apresenta várias características parametrizáveis:
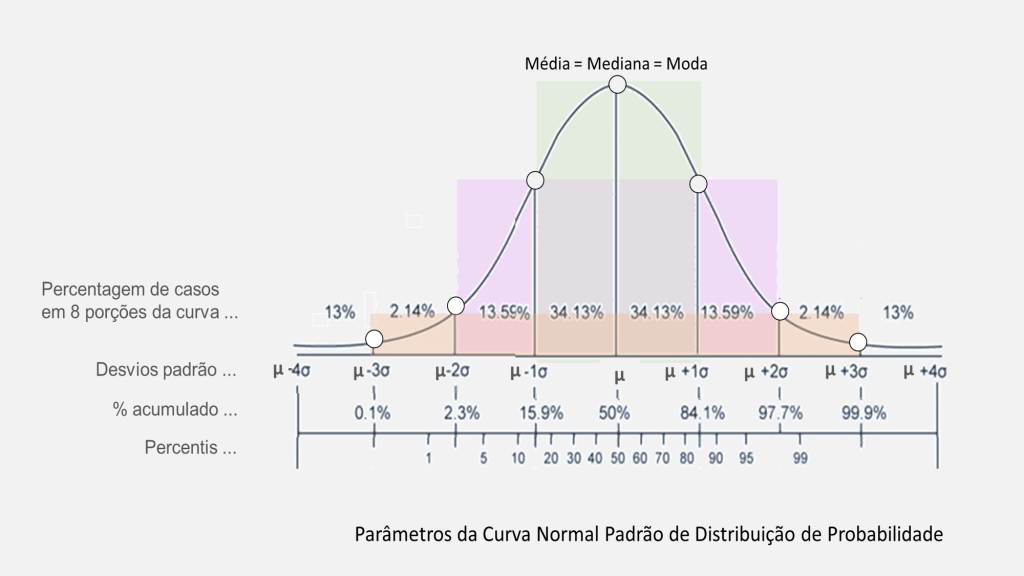
A média, mediana e média, medidadas de tendência central da estatúistica, na distribuição normal são iguais e posicionadas no “pico” ou ponto mais alto da curva de distribuição de probabilidade.
O gráfico da distribuição de probabilidade é cai simetricamente em torno da média.
Todas as distribuições normais podem ser descritas por apenas dois parâmetros: a média e o desvio padrão.
A média é o ponto mais alto da curva normal.
O desvio padrão é medida usada para quantificar a variabilidade da dispersão dos dados.
O desvio padrão é calculado como o nível de variação de dados em uma amostra em torno da média e define a largura da curva normal.
Usando a regra empírica, por exemplo, via pontuações de teste aleatórios. para grandes quantidades, 68% desses resultados devem estar dentro de um desvio padrão acima ou abaixo da média; afastar dois desvios padrão da média deve incluir 95% de todas as ocorrência e afstar três desvios padrão da média deve representar 99,7% das pontuações ( veja a figura acima ).
Cauda da Curva Normal
Em estatística descritiva, a curtose é uma medida de forma que caracteriza o achatamento da curva da função de distribuição de probabilidade
Curtose é uma medida estatística usada para descrever uma característica de uma curva normal.
Os dados plotados na curva normal mais distantes da média formam as caudas de cada lado da curva.
A curtose indica o quanto de dados residem nas caudas.
Curtose é uma medida de gordura das causas encontradas na distribuição de probabilidade.
Curtosis é uma medida do peso combinado das caudas de uma distribuição em relação ao centro da curva de distribuição ( a média ).
As distribuições com uma grande curtose têm mais dados de cauda do que os dados normalmente distribuídos, o que aproxima as duas caudas para a média; ao contrário, distribuições com baixa curtose têm menos dados de cauda, eafastar as caudas da média da curva normal.
Diante disso, alta curtose significa maior flutuação ou maior variância das ocorrências, numa dada amostra, o que representa. por exemplo, em análise de investimento um menor retorno sobre um dado investimento, longe dos retornos médios de investimentos.
Em finanças, o risco de curtose é também usado como medida da frequência com que o preço de um investimento se move dramaticamente; os investidores usam a distribuição de probabilidade normal dos retornos passados de uma ação para fazer suposições sobre retornos futuros esperados.
O Modelo Econômico Tradicional
O modelo econômico tradicionalmente utilizado pelas empresas é
dado pela expressão:
L = (P – V) . X – F
onde:
L = lucro total
P = preço unitário de venda do produto
V = custo variável por unidade
X = volume de vendas
F = custo fixo total
