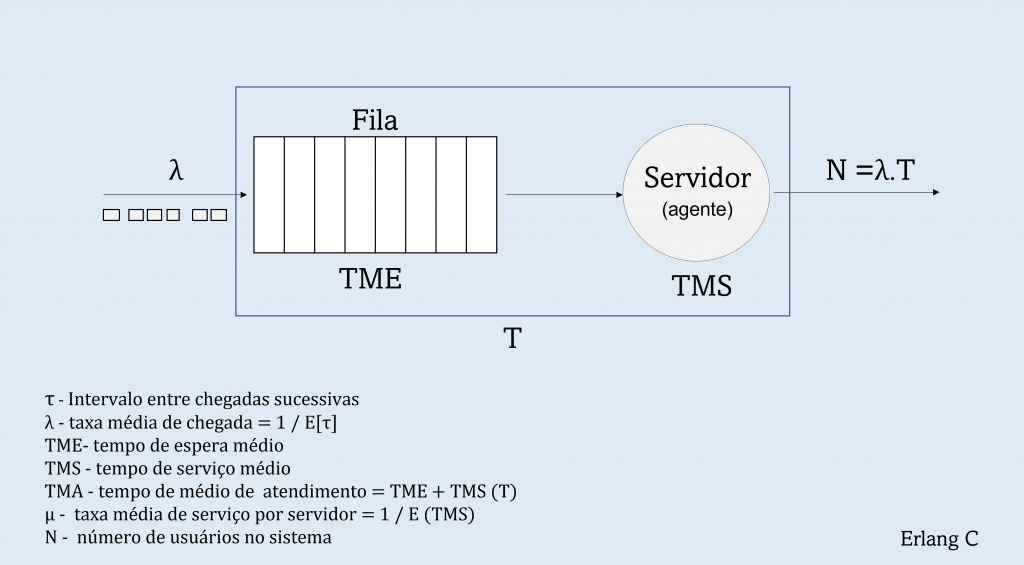
Na teoria das filas , uma disciplina dentro da probabilidade , a fila M/M/c (ou modelo Erlang–C é um modelo de filas multiservidor.
As chegadas formam uma única fila e são governadas por uma distribuição de probabilidade de Poisson , existem “c” servidores e os tempos de atendimento dos trabalhos são distribuídos exponencialmente.
É uma generalização da fila M/M/1 que considera apenas um único servidor.
Distribuição de Probabilidade de Poisson
A distribuição de Poisson representa um modelo matemático de processo estocástico (aleatório) muito usado para representar fenômenos da natureza, biológicos, sociais, mercados financeiros, etc, que parecem variar de forma não previsível.
É uma distribuição de probabilidade discreta que expressa a probabilidade de um determinado número de eventos ocorrer em um intervalo fixo de tempo ou espaço, se esses eventos ocorrerem com uma taxa média constante conhecida e independentemente do tempo desde o último evento; Pode ser usada para o número de eventos em outros tipos de intervalo especificados, como distância, área ou volume.
Diante disso, é usada na teoria de filas, para modelar eventos aleatórios, como a chegada de clientes a uma loja, telefonemas em uma central, caixas de supermercados, recursos compartilhados em rede, distribuição de objetos distribuídos numa área
A distribuição de Poisson tem a propriedade de que cada ponto (ocorrência do evento) é estocasticamente independente de todos os outros pontos do processo.
, razão pela qual às vezes é chamado de puramenteou processo completamente aleatório. [25] Modelar um sistema como um Processo de Poisson é insuficiente quando as interações ponto-a-ponto são muito fortes (isto é, os pontos não são estocasticamente independentes). Tal sistema pode ser melhor modelado com um processo de ponto diferente. [26]