Qualquer sistema de bens e serviços, é um sistema de “filas de espera” de recursos.
Teoria de filas é usada quando os recursos são compartilhados em rede … ou seja, na empresa, quase tudo!
Estuda formas de uso, otimização, dimensionamento e gestão de recursos em ambientes de demanda aleatórios.
Foca em “organizar e otimizar ” o acesso e uso de recursos ou ativos da empresa para bens e serviços.
Fila é uma característica de todo o ativo, que pelo menos tem uma fila de entrada, serviço, saída, na sua cadeia de valor.
Fila é um “sistema de espera”.
É usadas também além de conectar, priorizar e ajustar o fluxo de tarefas em rede e compartilhar recursos.
Pode ser modelada como uma caixa preta (ou nó), onde trabalhos chegam, esperam, são processados e são entregues.
O estudo das filas serve para modelar matematicamente um sistema ou tarefa, simular, diagnosticar e prognosticar o nível de serviço.
O “fator espera” é uma característica da fila e indicador de qualidade.
A fila e fator espera estão “umbilicados”, precisa ser previsíveis e controlados dentro da faixa de tolerância.
Filas estrututuram o sistemas mas afetam o humor das pessoas.
O que é Teoria de Filas
A teoria de filas é um ramo da matemática e probabilidade que estuda a formação, calculo, previsão e comprimentos de filas e tempo de espera.
Tem suas origens na pesquisa de Agner Krarup Erlang ( 1878 – 1929) quando criou modelos para descrever e dimensionar o sistema de telefonia na Dinamarca.
De lá para cá a inteligência de rede e artificial entrou em cena se desdobrou e alavancou e alavanca vários outros modelos sociais.
A teoria de filas define modelos para demonstrar o comportamento de um sistema em termos de taxa de chegada de serviço, tempo de servico e carga de trabalho, de forma precisa e útil para emprego na prática.
O objetivo é que um “determinado modelo de filas”, possa ser configurado para que os comprimentos das filas, tempo de espera, tempo de serviço, níveis de serviço , custos e valores, possam ser previstos e mantidos dentro de faixas de tolerância.
Teoria de filas contribui matematicamente para o dimensionamento de recursos, níveis de desempenho e qualidade de tarefas, bens e serviços.
É o estudo de modelos de fila e equacionar o tradeoff: Carga de trabalho, Taxa de chegada e Taxa de serviço.
Usa matemática e probabilidade para calcular capacidade, gargalos, em sistemas de filas em rede de recursos.
Estuda a parametrização, comportamento, dimensionamento de filas através de modelos matemáticos.
O uso da teoria de filas e matemáticas probabilísticas permite definir níveis de serviços e qualidade específico e mensuráveis.
É uma ferramenta para analisar a otimização de uso de recursos, bens e serviços em rede.
Equipa e melhora gestão de recursos, economia, atendimento, desempenho e segurança.
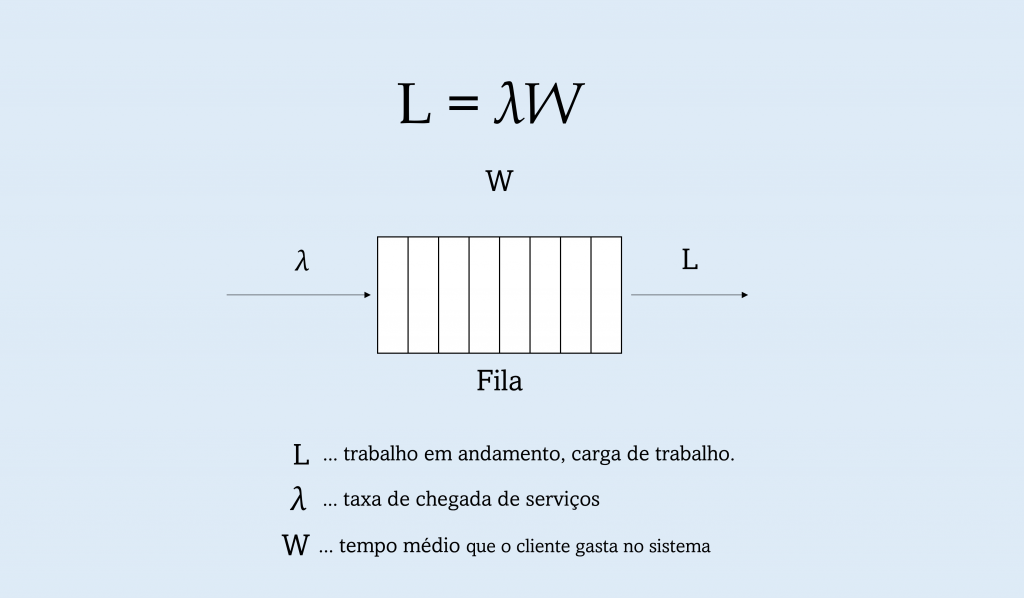
Lei de Little

O número médio de clientes no sistema L ( trabalho em andamento ou carga de trabalho, throughput, vazão), é igual a taxa média de chegada de serviços λ multiplicada pelo tempo médio que o cliente gasta no sistema W.

- Esse teorema simples, é baseado em médias de longo prazo, que podem ser registradas ao longo do tempo (minutos, horas, dias, semanas, meses).
- Quanto maior for o período de maturação e prática cada vez mais os resultados convergirão com maior precisão à fórmula.
- A sua aplicação e efetivação é conceitualmente simples e poderoza mas exige disciplina prática, gestão e balanceamento da teoria com a prática
Conclusão: um sistema de filas é definido e comparável por 3 variáveis: taxa de chegada, taxa de saída e tempo de serviço …
Premissas para a aplicação da Lei de Little
Sistema de filas estável … ou seja, carga de trabalho deve ter baixa variância.
Perído de Observação … para garantir que o sistema seja estacionário (não muda a distribuição de probabilidade do modelo ao longo do tempo).
Aplicações da Lei de Litlle
Calcular a faixa de operação e limites da equação L = λW
Modelar, simular e prever o comportamento de filas para L = λW
Analisar ou avaliar estratégias e táticas de movimentação de recursos para diferentes cenários e situações L = λW de um negócio.
Aplicar estratégias para reduzir tempo de serviço, taxa de abandono ou cancelamento de serviços.
Evitar ou minimizar gargalos mais prováveis.
Comparar diferentes sistemas e estratégias de tratamento de filas e gargalos.
Gerar planos de prevenção e reação para períodos de ociosidade ou sobrecarga dos sistemas produtivos.
Exemplos:
Cenário 1.
- Qual a CARGA de TRABALHO L, se W = 5 dias’ e λ = 5 serviços/ semana?
- Resposta: L = λW = 5 x 1, 43 = 7,15 serviços / dia
- (atentar conversão de unidade de tempo de semana para dia)
Cenário 2
- Qual o TEMPO de ATENDIMENTO W, se L = 8 atividades / dia e uma demanda λ de 5 serviços por semana?
- Resposta: W = L/λ = 8/1,43 = 5,6 dias
Cenário 3
- Pergunta: Qual o impacto em W, se reduzirmos L de 8 para 5 serviços semans por e λ mantido em 1,4, no tempo de espera W?
- Resposta: W= 3,5 dias.
Fundamentos da Teoria de filas
Processo de Chegada (demanda)
- O intervalo entre chegadas é uma variável aleatória fundamental que modela qualquer fila.
- As distribuição de probabilidade de chegada de fenômenos e serviços mais comum é a de Poisson , onde intervalos de chegada são distribuídos exponencialmente.
- Existem outras distribuições frequentes, como a determinística, genérica, etc.
Processo de Serviço (oferta)
- O tempo que cada usuário do sistema de fila passa em serviço define o tempo de serviço (lead time, tempo de atendimento)
- É razoável considerar esses tempos de serviço como “variáveis aleatória” independentes e identicamente distribuídos.
- A distribuição mais comum para o processo de serviço é a exponencial, mas também existem outras, ta, como o processo de chegada.
Número de Servidores
- Determina o número de servidores normalmente idênticos.
Capacidade do Sistema
- Quantidade máxima de usuários no sistema (fila + serviços).
Tamanho da População
- Quantidade total de usuários potenciais que podem chegar ao sistema de filas.
Disciplina de Serviço
Ordem de atendimento de usuários do sistema.
- FIFO – First In First Out. Primeiro a chegar é o primeiro a ser atendido.
- RR – Round Robin. Atendimento por um tempo máximo e se não finalizado vai pro final da fila.
- LCFS – Last Come First Served … último a chegar é o primeiro a ser servido.
- LCFS – preemptivo – o último usuário pode interromper o que está sendo atendido.
- COMPARTILHAMENTO … Repartir o o processador em n partes iguais.
Parametrização de um Sistema de filas
A/S/m/B/K/SD
A – distribuição dos intervalos de chegada
- M – exponencial ... sem memória” – o estado atual não depende dos anteriores; se os intervalos entre chegadas são distribuídos expeonencialmente com média 1/λ tempo esperado para a próxima chegada é sempre 1/λ, independente do tempo que ja transcorreu desde a última chegada.
- D – determinística … tempos constantes entre chegadas e sem variabilidade.
- G – genérica …não especificada e resultados válidos para qualquer distribuição.
S – distribuição dos tempos de serviço.
m – número de servidores.
B – número máximo de usuários no sistema.
K – tamanho máximo da população
SD – disciplina de atendimento ou serviço
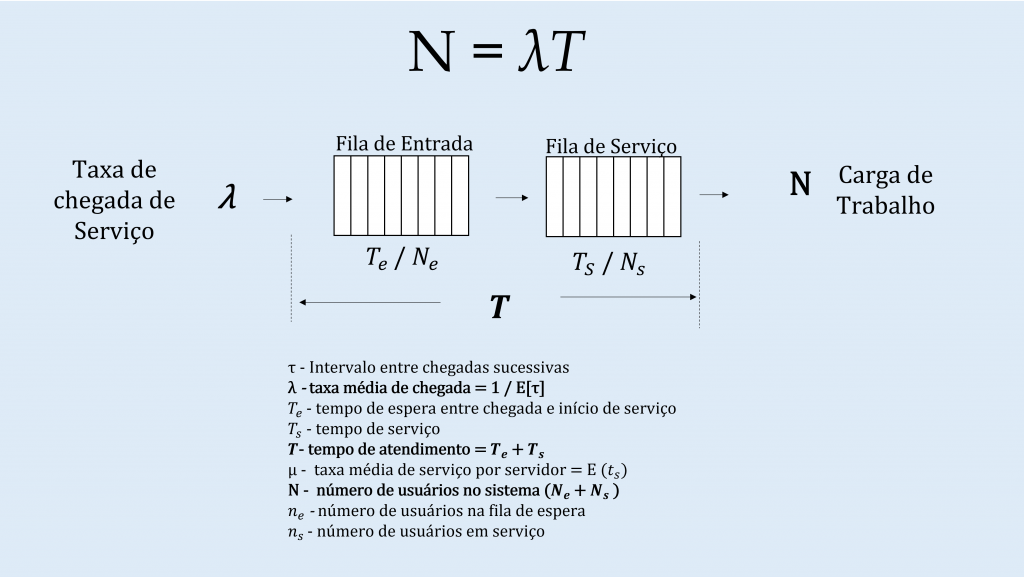
τ – Intervalo entre chegadas sucessivas
λ – taxa média de chegada = 1 / E[τ]
T_(e )- tempo de espera entre chegada e início de serviço
T_s – tempo de serviço
T– tempo de atendimento = T_(e )+ T_s
µ – taxa média de serviço por servidor = E (t_s)
N – número de usuários no sistema (N_(e )+ N_(s ))
n_(e )– número de usuários na fila de espera n_(s )- número de usuários em serviço

Quais são as principais filas de serviço que convivemos?
Como dimensionar sistemas de filas?
Como modelar, simular, usar, controlar e ajustar um sistema de filas?
Como comparar dois sistemas de filas?
Quais são as principais filas de pessoas, clientes, objetos, atividades e tarefas na empresa?