Frequentemente a solução para um mesmo problema matemático pode ser encontrada geometricamente, algebricamente ou analiticamente.
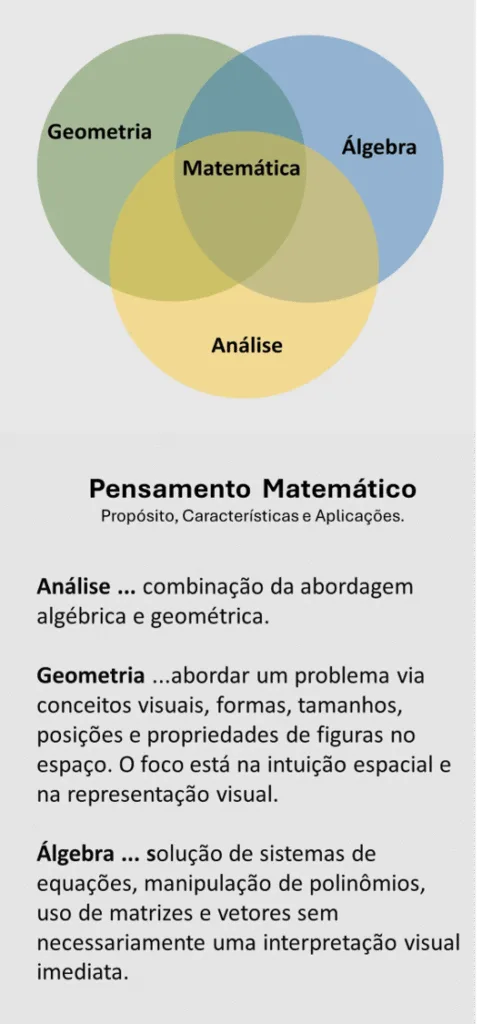
Análise … combinar abordagem algébrica e geométrica … técnica de dividir o todo em partes menores e mais fáceis de serem resolvidas; desamarrar; enumerar, evidenciar, compreender, simbolizar; usar a matemática, lógica, álgebra e geometria.
Geometria … abordar um problema via conceitos visuais, formas, tamanhos, posições e propriedades de figuras no espaço. O foco está na intuição espacial e na representação visual.
Álgebra … solucionar sistemas de equações, manipulação de números e polinômios, uso de matrizes e vetores sem necessariamente uma interpretação visual imediata.

Conclusão.
- A matemática de uma forma geral apresenta três formas diferentes de pensar e resolver problemas … análise, álgebra e geometria.
- A decisão sobre qual é a melhor forma de resolver o problema matematicamente é subjetiva, depende do contexto e do desenvolvimento de habilidades de cada indivíduo.
- O ideal é o equilíbrio, flexibilidade e visão metacognitiva (ou tática cognitiva) para diferenciar situações e “acionar” as melhores formas de linguagem e ferramentas de resolução de problemas.
- Cada uma das visões agrega valor a atuam de forma complementar e sinérgica.
- Saiba mais sobre análise, álgebra e geometria e aplicações na empresa.